题目内容
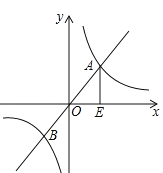
【题目】如图，四边形ABCD是菱形，点D的坐标是（0，
），以点C为顶点的抛物线y＝ax2+bx+c恰经过x轴上的点A，B．
（1）求点C的坐标；
（2）若抛物线向上平移后恰好经过点D，求平移后抛物线的解析式．
【答案】
【1】 (1)．C的坐标（2，
）
【2】 (2)．y=-x2+4x+
【解析】
（1）连接AC，在菱形ABCD中，CD∥AB，AB=BC=CD=DA，由抛物线对称性可知AC=BC．∴△ABC，△ACD都是等边三角形．可求CD=AD=
=2，可得点C的坐标为（2，
）．
（2）由抛物线y=ax2+bx+c的顶点为（2，），可设抛物线的解析式为：y=a(x?2)2+
由（1）可得A（1，0），把A（1，0）代入上式，解得a=-，设平移后抛物线的解析式为y=-（x-2）2+k，把（0，）代入上式得K=5．即可得到平移后抛物线的解析式．
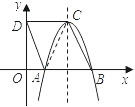
解：（1）连接AC，在菱形ABCD中，CD∥AB，
AB=BC=CD=DA，
由抛物线对称性可知AC=BC．（1分）
∴△ABC，△ACD都是等边三角形．
∴CD=AD==2（2分）
∴点C的坐标为（2，）．（3分）
（2）由抛物线y=ax2+bx+c的顶点为（2，），
可设抛物线的解析式为．y=a(x?2)2+
由（1）可得A（1，0），把A（1，0）代入上式，
解得a=-．（5分）
设平移后抛物线的解析式为y=-（x-2）2+k，
把（0，）代入上式得K=5．
∴平移后抛物线的解析式为：
y=-（x-2）2+5（7分）
即y=-x2+4x+．
练习册系列答案
相关题目
