Question

【题目】抛物线的顶点为（1，﹣4），与x轴交于A、B两点，与y轴负半轴交于C（0，﹣3）．

（1）求抛物线的解析式；

（2）点P为对称轴右侧抛物线上一点，以BP为斜边作等腰直角三角形，直角顶点M落在对称轴上，求P点的坐标．

Answer 1

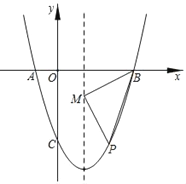
【答案】（1）y＝x2﹣2x﹣3；（2）点P的坐标为（2，﹣3）或（4，5）．

【解析】

（1）由抛物线的顶点坐标可设抛物线的解析式为y=a（x-1）2-4，代入点C的坐标可求出a值，进而可得出抛物线的解析式；
（2）利用二次函数图象上点的坐标特征可求出点A，B的坐标，设抛物线对称轴与x轴交于点E，过点P作PF∥x轴，交抛物线对称轴于点F，易证△MBE≌△PMF，根据全等三角形的性质可得出ME=PF=x-1，MF=BE=2，进而可得出EF=x+1，结合EF为点P纵坐标的绝对值，即可得出关于x的一元二次方程，解之即可求出x的值，取其大于1的值代入点P的坐标中即可得出结论．

解：（1）设抛物线的解析式为y＝a（x﹣1）2﹣4，

将C（0，﹣3）代入y＝a（x﹣1）2﹣4，得：﹣3＝a（0﹣1）2﹣4，

解得：a＝1，

∴抛物线的解析式为y＝（x﹣1）2﹣4＝x2﹣2x﹣3．

（2）当y＝0时，有x2﹣2x﹣3＝0，

解得：x1＝﹣1，x2＝3，

∴点A的坐标为（﹣1，0），点B的坐标为（3，0）．

设抛物线对称轴与x轴交于点E，过点P作PF∥x轴，交抛物线对称轴于点F，如图所示．

设点P的坐标为（x，x2﹣2x﹣3）（x＞1），则PF＝x﹣1，BE＝3﹣1＝2．

∵∠BME+∠PMF＝90°，∠BME+∠MBE＝90°，

∴∠MBE＝∠PMF．

在△MBE和△PMF中， ，

∴△MBE≌△PMF（AAS），

∴ME＝PF＝x﹣1，MF＝BE＝2，

∴EF＝ME+MF＝x+1．

∵EF＝|x2﹣2x﹣3|，

∴|x2﹣2x﹣3|＝x+1，即x2﹣3x﹣4＝0或x2﹣x﹣2＝0，

解得：x1＝﹣1（舍去），x2＝2，x3＝4，

∴点P的坐标为（2，﹣3）或（4，5）．