题目内容
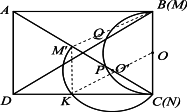
矩形ABCD中,AD=2,2<AB<4,现将一个直径MN为2的量角器如图1摆放,使其0°线的端点N与C重合,M与B重合,O为MN的中点,量角器的半圆弧与矩形ABCD的对角线AC、BD分别交于P、Q,设P、Q在量角器上的读数分别是x、y.
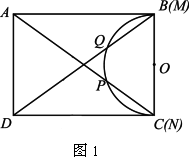
(1)求y与x之间的函数关系式.(不必写出自变量的取值范围).
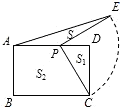
(2)将量角器绕C点逆时针旋转,使它的直径落在AC上,如图2所示,![]() 为
为![]() 的中点,此时量角器的半圆弧交DC于K,若K点的读数为z,那么z与y的数量关系是什么,请说明理由.
的中点,此时量角器的半圆弧交DC于K,若K点的读数为z,那么z与y的数量关系是什么,请说明理由.
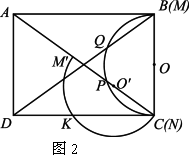
(3)如图2所示,若![]() ∥KO,求出此时AB的长.
∥KO,求出此时AB的长.
解析:
|
解: (1)连结OQ、OP ∵ABCD是矩形, ∴AC=BD. ∴BE=CE. ∴∠EBO=∠OCE ∵OQ=OB, ∴∠EBO=∠OQB. ∴∠BOQ=180°-2∠EBO. 同理可证 ∠COP=180°-2∠OCE. ∴∠BOQ=∠COP=x°. 2分 ∴y°=∠COQ=180°-∠BOQ=180°-x° ∴y=180-x. 3分
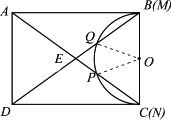
(2)z与y的数量关系是:z=y 4分 如下图,连结 ∵∠ACD+∠BCA=90°, ∴∠ACD=90°-∠BCA. ∴z°=180°-2∠ACD =180°-2(90°-∠BCA ) =2∠BCA =180°-∠COP. ∴z=180-x. ∵y=180-x, ∴z=y. 5分
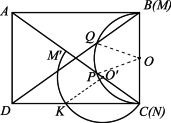
(3)如下图,连结B ∵ ∴∠ ∵∠BCD=90°, ∴∠ ∴BO∥ ∵ ∴ ∴ ∵ ∴ ∴∠ACD=30°. 7分 ∴AC=4 ∴
∴ 在Rt△ADC中, ∵AD=2, ∴DC=2 ∵ABCD是矩形, ∴DC=AB=2
|

| A、10° | B、15° | C、22.5° | D、30° |
 如图,在矩形ABCD中,AD=30,AB=20,若点E、F三等分对角线AC,则△ABE的面积为( )
如图,在矩形ABCD中,AD=30,AB=20,若点E、F三等分对角线AC,则△ABE的面积为( )| A、60 | B、100 | C、150 | D、200 |

 在矩形ABCD中,AD=4,点P在AD上,且AP:PD=a:b
在矩形ABCD中,AD=4,点P在AD上,且AP:PD=a:b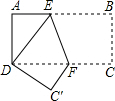 已知:如图,矩形ABCD中,AD=4cm,AB=8cm,按如图方式折叠,使点B与点D重合,折痕为EF.求EF的长.
已知:如图,矩形ABCD中,AD=4cm,AB=8cm,按如图方式折叠,使点B与点D重合,折痕为EF.求EF的长.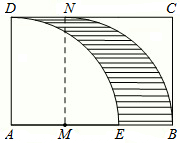 如图,矩形ABCD中,AD=2,AB=3,AM=1,
如图,矩形ABCD中,AD=2,AB=3,AM=1,