题目内容
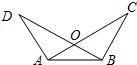 17、如图,∠BAC=∠ABD,请你添加一个条件:
17、如图,∠BAC=∠ABD,请你添加一个条件:∠C=∠D或∠ABC=∠BAD或AC=BD或∠OBC=∠OAD
,使BC=AD(只添一个条件即可).
分析:若使BC=AD,则可证明△DAB≌△CBA,有已知条件可知:缺少的条件可以是一对角或一对边,所以添加∠C=∠D问题可得证.
解答:可添加的条件为:∠C=∠D.
证明:∵∠BAC=∠ABD,∠C=∠D,AB=BA,
∴△BAC≌△ABD(AAS).
∴BC=AD.
故答案为:∠C=∠D.
证明:∵∠BAC=∠ABD,∠C=∠D,AB=BA,
∴△BAC≌△ABD(AAS).
∴BC=AD.
故答案为:∠C=∠D.
点评:本题考查了全等三角形的判,常用的判断方法为:SAS,SSS,AAS,ASA.在证明中还要注意图形中隐藏条件的挖掘如:本题中的公共边AB.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
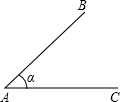 如图,∠BAC=45°,AB=4.现请你给定线段BC的长,使△ABC能构成等腰三角形.则BC的长可以是( )
如图,∠BAC=45°,AB=4.现请你给定线段BC的长,使△ABC能构成等腰三角形.则BC的长可以是( )| A、4 | ||
B、2
| ||
C、4或2
| ||
D、4或
|
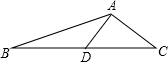 如图,∠BAC=120°,AD⊥AC,BD=CD,则下列结论正确的是( )
如图,∠BAC=120°,AD⊥AC,BD=CD,则下列结论正确的是( )| A、AD=AC | ||
B、AB=
| ||
| C、AB=2AC | ||
D、AB=
|
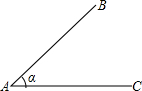 如图,∠BAC=45°,AB=6.现请你给定线段BC的长,使构成△ABC能构成等腰三角形.则BC的长可以是
如图,∠BAC=45°,AB=6.现请你给定线段BC的长,使构成△ABC能构成等腰三角形.则BC的长可以是
 如图,∠BAC=∠ABD,BD、AC交于点O,要使OC=OD,还需添加一个条件,这个条件可以是
如图,∠BAC=∠ABD,BD、AC交于点O,要使OC=OD,还需添加一个条件,这个条件可以是