题目内容
 用两个全等的正方形ABCD和DCEF拼成一个矩形ABEF,把一个足够大的直角三角尺的直角顶点与这个矩形的边AF的中点D重合,且将直角三角尺绕点D按顺时针方向旋转.探究:
用两个全等的正方形ABCD和DCEF拼成一个矩形ABEF,把一个足够大的直角三角尺的直角顶点与这个矩形的边AF的中点D重合,且将直角三角尺绕点D按顺时针方向旋转.探究:当直角三角尺的两直角边分别与矩形ABEF的两边BE,EF相交于点G,H时,如图,通过观察或测量BG与EH的长度,你能得到什么结论?证明你的结论.
分析:BG=EH.通过全等三角形△DCG≌△DFH的对应边相等证得CG=FH,则易证BG=EH.
解答: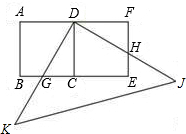 解:BG=EH.理由如下:
解:BG=EH.理由如下:
∵正方形ABCD和DCEF全等,
∴CD=DF,∠BCD=∠DFE=90°即∠GCD=∠HFD=90°,
又∵∠KDJ=90°,
∴∠GDC=∠HDF,
∴在△DCG与△DFH中,
,
∴△DCG≌△DFH(ASA),
∴CG=FH,
∴BC-GC=EF-FH,即BG=EH.
 解:BG=EH.理由如下:
解:BG=EH.理由如下:∵正方形ABCD和DCEF全等,
∴CD=DF,∠BCD=∠DFE=90°即∠GCD=∠HFD=90°,
又∵∠KDJ=90°,
∴∠GDC=∠HDF,
∴在△DCG与△DFH中,
|
∴△DCG≌△DFH(ASA),
∴CG=FH,
∴BC-GC=EF-FH,即BG=EH.
点评:本题考查了全等三角形的判定与性质.全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 23、用两个全等的正方形ABCD和CDFE拼成一个矩形ABEF,把一个足够大的直角三角尺的直角顶点与这个矩形的边AF的中点D重合,且将直角三角尺绕点D按逆时针方向旋转.
23、用两个全等的正方形ABCD和CDFE拼成一个矩形ABEF,把一个足够大的直角三角尺的直角顶点与这个矩形的边AF的中点D重合,且将直角三角尺绕点D按逆时针方向旋转. 25、友情提示:本题有A、B两题,请你任选一题作答,A题满分9分,B题满分12分.若两题都做,只能按A题评分.
25、友情提示:本题有A、B两题,请你任选一题作答,A题满分9分,B题满分12分.若两题都做,只能按A题评分.

