题目内容
如图：△ABC的边AB的垂直平分线分别交BC、AB于M、N，△ACM的周长为10cm，AN=4cm．则△ABC的周长是（ ）cm．分析：由△ABC的边AB的垂直平分线分别交BC、AB于M、N，根据线段垂直平分线的性质，可得AM=BM，又由△ACM的周长为10cm，AN=4cm，可求得AC+BC与AB的长，继而求得答案．
解答：解：∵MN是AB的垂直平分线，
∴AM=BM，
∵△ACM的周长为10cm，
∴AC+CM+AM=AC+CM+BM=AC+BC=10cm，
∵AN=4cm，
∴AB=2AN=8（cm），
∴△ABC的周长为：AB+AC+BC=18（cm）．
故选C．
∴AM=BM，
∵△ACM的周长为10cm，
∴AC+CM+AM=AC+CM+BM=AC+BC=10cm，
∵AN=4cm，
∴AB=2AN=8（cm），
∴△ABC的周长为：AB+AC+BC=18（cm）．
故选C．
点评：此题考查了线段垂直平分线的性质．此题难度不大，注意掌握转化思想与整体思想的应用．
练习册系列答案
相关题目
25、如图，△ABC的边AB、AC上分别有定点M、N，请在BC边上找一点P，使得△PMN的周长最短． （写出作法，保留作图痕迹）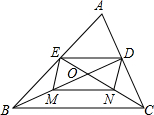
如图，△ABC的边AC、AB上的中线BD、CE相交于点O，M、N分别是BO、CO的中点，顺次连接点D、E、M、N．
如图，△ABC的边BC的垂直平分线MN交AC于D，若AC=6cm，AB=4cm，则△ADB的周长=
如图，△ABC的边BC上的高为AD，且BC=9cm，AD=2cm，AB=6cm．