题目内容
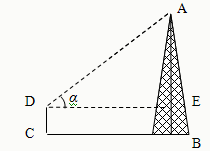
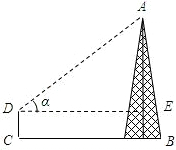 如图,小明为测量某铁塔AB的高度,他在离塔底B的10米C处测得塔顶的仰角α=43°,已知小明的测角仪高CD=1.5米,求铁塔AB的高.(精确到0.1米)
如图,小明为测量某铁塔AB的高度,他在离塔底B的10米C处测得塔顶的仰角α=43°,已知小明的测角仪高CD=1.5米,求铁塔AB的高.(精确到0.1米)(参考数据:sin43°=0.6820,cos43°=0.7314,tan43°=0.9325)
分析:本题是一个直角梯形的问题,可以过点D作DE⊥AB于点E,把求AB的问题转化求AE的长,从而可以在△ADE中利用三角函数求解.
解答:解:如图,可知四边形DCBE是矩形.
∴EB=DC=1.5米,DE=CB=10米.
在Rt△AED中,∠ADE=α=43°.
∴tanα=
.
∴AE=DE•tan43°=10×0.9325=9.325米;
∴AB=AE+EB=9.325+1.5=10.825≈10.8(米).
∴EB=DC=1.5米,DE=CB=10米.
在Rt△AED中,∠ADE=α=43°.
∴tanα=
| AE |
| DE |
∴AE=DE•tan43°=10×0.9325=9.325米;
∴AB=AE+EB=9.325+1.5=10.825≈10.8(米).
点评:解直角梯形可以通过作高线转化为解直角三角形和矩形的问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
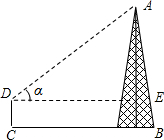 如图,小明为测量某铁塔AB的高度,他处测得塔顶的仰角已知小明的测角仪高CD=1.5米,求铁塔AB的高.(精确到0.1米(参考数据:sin43°=0.6820,cos43°=0.7314,tan43°=0.9325)
如图,小明为测量某铁塔AB的高度,他处测得塔顶的仰角已知小明的测角仪高CD=1.5米,求铁塔AB的高.(精确到0.1米(参考数据:sin43°=0.6820,cos43°=0.7314,tan43°=0.9325)