ЬтФПФкШн
ЁОЬтФПЁПШчЭМ1ЃЌдкЬнаЮABCDжаЃЌABЁЮCDЃЌЁЯB=90ЁуЃЌAB=2ЃЌCD=1ЃЌBC=mЃЌPЮЊЯпЖЮBCЩЯЕФвЛЖЏЕуЃЌЧвКЭBЁЂCВЛжиКЯЃЌСЌНгPAЃЌЙ§PзїPEЁЭPAНЛCDЫљдкжБЯпгкEЃЎЩшBP=xЃЌCE=yЃЎ

ЃЈ1ЃЉЧѓyгыxЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉШєЕуPдкЯпЖЮBCЩЯдЫЖЏЪБЃЌЕуEзмдкЯпЖЮCDЩЯЃЌЧѓmЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌШєm=4ЃЌНЋЁїPECбиPEЗелжСЁїPEGЮЛжУЃЌЁЯBAG=90ЁуЃЌЧѓBPГЄЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]()
ЃЈ2ЃЉ0ЃМ![]()
ЃЈ3ЃЉBPЕФГЄЮЊ![]() Лђ2
Лђ2
ЁОНтЮіЁП
ЗжЮіЃКЃЈ1ЃЉжЄУїЁїABPЁзЁїPCEЃЌРћгУБШР§ЯпЖЮЙиЯЕЧѓГіyгыxЕФКЏЪ§ЙиЯЕЪНЁЃ
ЃЈ2ЃЉИљОнЃЈ1ЃЉжаЧѓГіЕФyгыxЕФЙиЯЕЪНЃЌРћгУЖўДЮКЏЪ§аджЪЃЌЧѓГіЦфзюДѓжЕЃЌСаВЛЕШЪНШЗЖЈmЕФШЁжЕЗЖЮЇЁЃ
ЃЈ3ЃЉИљОнЗелЕФаджЪМАвбжЊЬѕМўЃЌЙЙдьжБНЧШ§НЧаЮЃЌРћгУЙДЙЩЖЈРэЧѓГіBPЕФГЄЖШЁЃ
НтЃКЃЈ1ЃЉЁпЁЯAPB+ЁЯCPE=90ЁуЃЌЁЯCEP+ЁЯCPE=90ЁуЃЌЁрЁЯAPB=ЁЯCEPЁЃ
гжЁпЁЯB=ЁЯC=90ЁуЃЌЁрЁїABPЁзЁїPCEЁЃ
Ёр![]() ЃЌМД
ЃЌМД![]() ЁЃ
ЁЃ
ЁрyгыxЕФКЏЪ§ЙиЯЕЪНЮЊ![]() ЁЃ
ЁЃ
ЃЈ2ЃЉЁп![]() ЃЌ
ЃЌ
ЁрЕБx=![]() ЪБЃЌyШЁЕУзюДѓжЕЃЌзюДѓжЕЮЊ
ЪБЃЌyШЁЕУзюДѓжЕЃЌзюДѓжЕЮЊ![]() ЁЃ
ЁЃ
ЁпЕуPдкЯпЖЮBCЩЯдЫЖЏЪБЃЌЕуEзмдкЯпЖЮCDЩЯЃЌ
Ёр![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЁЃ
ЁЃ
ЁпmЃО0ЃЌЁрmЕФШЁжЕЗЖЮЇЮЊЃК0ЃМ![]() ЁЃ
ЁЃ
ЃЈ3ЃЉгЩелЕўПЩжЊЃЌPG=PCЃЌEG=ECЃЌЁЯGPE=ЁЯCPEЃЌ
гжЁпЁЯGPE+ЁЯAPG=90ЁуЃЌЁЯCPE+ЁЯAPB=90ЁуЃЌ
ЁрЁЯAPG=ЁЯAPBЁЃ
ЁпЁЯBAG=90ЁуЃЌЁрAGЁЮBCЁЃЁрЁЯGAP=ЁЯAPBЁЃ
ЁрЁЯGAP=ЁЯAPGЁЃЁрAG=PG=PCЁЃ
ШчЭМЃЌЗжБ№бгГЄCEЁЂAGЃЌНЛгкЕуHЃЌ
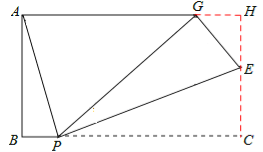
дђвзжЊABCHЮЊОиаЮЃЌHE=CHЉCE=2ЉyЃЌ![]() ЃЌ
ЃЌ
дкRtЁїGHEжаЃЌгЩЙДЙЩЖЈРэЕУЃКGH2+HE2=GH2ЃЌ
МДЃКx2+ЃЈ2ЉyЃЉ2=y2ЃЌЛЏМђЕУЃКx2Љ4y+4=0 Ђй
гЩЃЈ1ЃЉПЩжЊ![]() ЃЌетРяm=4ЃЌЁр
ЃЌетРяm=4ЃЌЁр![]() ЁЃ
ЁЃ
ДњШыЂйЪНећРэЕУЃКx2Љ8x+4=0ЃЌНтЕУЃКx=![]() Лђx=2ЁЃ
Лђx=2ЁЃ
ЁрBPЕФГЄЮЊ![]() Лђ2ЁЃ
Лђ2ЁЃ

ЁОЬтФПЁПдкбЇаЃзщжЏЕФЩчЛсЪЕМљЛюЖЏжаЃЌЕквЛаЁзщИКд№ЕїВщШЋаЃ10000УћЭЌбЇУПЬьЭъГЩМвЭЅзївЕЪБМфЧщПіЃЌЫћУЧЫцЛњГщШЁСЫвЛВПЗжЭЌбЇНјааЕїВщЃЌОЎЛцжЦСЫЫљГщШЁбљБОЕФЦЕЪ§ЗжВМБэКЭЖюЪ§ЗжВМжБЗНЭМ(ШчЭМ).
ЪБМфxЃЈаЁЪБЃЉ | ЦЕЪ§ | АйЗжБШ |
0.5Ёмx<1 | 4 | 8ЃЅ |
1Ёмx<1.5 | 5 | 10ЃЅ |
1.5Ёмx<2 | a | 40ЃЅ |
2Ёмx<2.5 | 15 | 30ЃЅ |
2.5Ёмx<3 | 4 | 8ЃЅ |
xЁн3 | 2 | b |
ЦЕЪ§ЗжВМБэ

ЧыИљОнЭМжааХЯЂНтД№ЯТСаЮЪЬтЃК
(1)ИУаЁзщвЛЙВГщВщСЫ___________ШЫЃЛ
(2)ЦЕЪ§ЗжВМБэжаЕФa=___________ЃЌb=____________ЃЛ
(3)НЋЦЕЪ§ЗжВМжБЗНЭМВЙГфЭъећ(жБНгЛЭМЃЌВЛаДМЦЫуЙ§ГЬ)ЃЛ
(4)ЁЖСЩФўЪЁТфЪЕНЬг§ВПЕШОХВПУХЙигкжааЁбЇЩњМѕИКДыЪЉЪЕЪЉЗНАИЁЗЙцЖЈЃЌГѕжаЩњУПЬьЪщУцМвЭЅзївЕЪБМфВЛГЌЙ§1.5аЁЪБЃЌИљОнБэжаЪ§ОнЃЌЧыФуЬсГіКЯРэЛЏНЈвщ.








