题目内容
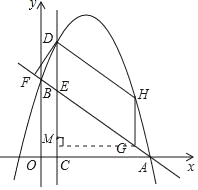
【题目】如图,已知二次函数y=ax2﹣(2a﹣![]() )x+3的图象经过点A(4,0),与y轴交于点B.在x轴上有一动点C(m,0)(0<m<4),过点C作x轴的垂线交直线AB于点E,交该二次函数图象于点D.
)x+3的图象经过点A(4,0),与y轴交于点B.在x轴上有一动点C(m,0)(0<m<4),过点C作x轴的垂线交直线AB于点E,交该二次函数图象于点D.
(1)求a的值和直线AB的解析式;
(2)过点D作DF⊥AB于点F,设△ACE,△DEF的面积分别为S1,S2,若S1=4S2,求m的值;
(3)点H是该二次函数图象上位于第一象限的动点,点G是线段AB上的动点,当四边形DEGH是平行四边形,且DEGH周长取最大值时,求点G的坐标.

【答案】(1)y=﹣![]() ;(2)m值为
;(2)m值为![]() ;(3)点G坐标为(
;(3)点G坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)
【解析】
(1)把点A坐标代入y=ax2﹣(2a﹣![]() )x+3可求a,用待定系数法求直线AB的解析即可;(2)用含有m的代数式表示DE、AC的长,易证△DEF∽△AEC,S1=4S2,得到DE与AE的数量关系可以构造方程,解方程即可求得m的值;
)x+3可求a,用待定系数法求直线AB的解析即可;(2)用含有m的代数式表示DE、AC的长,易证△DEF∽△AEC,S1=4S2,得到DE与AE的数量关系可以构造方程,解方程即可求得m的值;
(3)如图,过点G做GM⊥DC于点M,用含有n的代数式表示GH,由平行四边形性质DE=GH,可得m,n之间数量关系,利用相似用GM表示EG,即可用含有m的代数式表示DEGH周长,利用函数性质求出周长最大时的m值,可得n值,进而求G点坐标.
(1)把点A(4,0)代入,得0=a42﹣(2a﹣![]() )×4+3,
)×4+3,
解得a=﹣![]() ,
,
∴函数解析式为:y=![]() ;
;
设直线AB解析式为y=kx+b,
把A(4,0),B(0,3)代入得![]() ,
,
解得![]() ;
;
∴直线AB解析式为:y=﹣![]() ;
;
(2)由已知,点D坐标为(m,﹣![]() ),点E坐标为(m,﹣
),点E坐标为(m,﹣![]() ),
),
∴AC=4﹣m,DE=(﹣![]() )﹣(﹣
)﹣(﹣![]() )=﹣
)=﹣![]() ,
,
∵BC∥y轴,
∴![]() ,
,
∴AE=![]() ,
,
∵∠DFA=∠DCA=90°,∠FBD=∠CEA,
∴△DEF∽△AEC;
∵S1=4S2,
∴AE=2DE,
∴![]() ,
,
解得m1=![]() ,m2=4(舍去),
,m2=4(舍去),
故m值为![]() ;
;
(3)如图,过点G做GM⊥DC于点M,
由(2)DE=﹣![]() ,同理HG=﹣
,同理HG=﹣![]() ;
;
∵四边形DEGH是平行四边形,
∴﹣![]() =﹣
=﹣![]() ,
,
整理得:(n﹣m)[![]() ]=0,
]=0,
∵m≠n,
∴m+n=4,即n=4﹣m,
∴MG=n﹣m=4﹣2m
由已知△EMG∽△BOA,
∴![]() ,
,
∴EG=![]() ,
,
∴DEGH周长L=2[﹣![]() +
+![]() ]=﹣
]=﹣![]() ,
,
∵a=﹣![]() <0,
<0,
∴m=﹣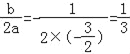 时,L最大.
时,L最大.
∴n=4﹣![]() =
=![]() ,
,
∴G点坐标为(![]() ,
,![]() ),此时点E坐标为(
),此时点E坐标为(![]() ,
,![]() ),
),
当点G、E位置对调时,依然满足条件,
∴点G坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)






