��Ŀ����
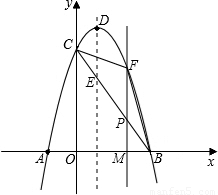
��ͼ��������y=-x2+2x+3��x���ཻ��A��B���㣨��A�ڵ�B����ࣩ����y���ཻ�ڵ�C������ΪD����1��ֱ��д��A��B��C���������������ߵĶԳ��
��2������BC���������ߵĶԳ��ύ�ڵ�E����PΪ�߶�BC�ϵ�һ�����㣬����P��PF��DE���������ڵ�F�����P�ĺ�����Ϊm��
���ú�m�Ĵ���ʽ��ʾ�߶�PF�ij����������mΪ��ֵʱ���ı���PEDFΪƽ���ı��Σ�
�����BCF�����ΪS����S��m�ĺ�����ϵʽ��

���𰸡���������1����֪�������ߵĽ���ʽ����y=0ʱ�����A��B��������꣬��x=0ʱ�������C������꣮���ݶԳ���x=-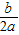 �ɵó��Գ���Ľ���ʽ��
�ɵó��Գ���Ľ���ʽ��
��2��PF�ij����ǵ�x=mʱ�������ߵ�ֵ��ֱ��BC����һ�κ�����ֵ�IJ���ȸ���B��C���������BC����ֱ�ߵĽ���ʽ��Ȼ��m�ֱ����ֱ��BC�������ߵĽ���ʽ�У���ó���������ֵ�IJ����PF�ij���
����ֱ��BC�Ľ���ʽ���ɵó�E������꣬���������ߵĽ���ʽ�����D������꣬Ȼ���������ϵ������ľ��빫ʽ�������DE�ij���Ȼ����PF=DE�����������ʱm��ֵ��
��3���ɽ�������BCF�ֳ�����������
һ������������PFC����PFΪ�ױߣ���P�ĺ�����Ϊ���ɵó�������PFC�������
һ������������PFB����PFΪ�ױߣ���P��B����ĺ������ľ���ֵΪ�ߣ��������������PFB�������
Ȼ�����������BCF�����=������PFC�����+������PFB����������������S��m�ĺ�����ϵʽ��
��� �⣺��1��A��-1��0����B��3��0����C��0��3����
�⣺��1��A��-1��0����B��3��0����C��0��3����
�����ߵĶԳ����ǣ�ֱ��x=1��
��2������ֱ��BC�ĺ�����ϵʽΪ��y=kx+b��
��B��3��0����C��0��3���ֱ����ã�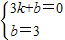
��ã�k=-1��b=3��
����ֱ��BC�ĺ�����ϵʽΪ��y=-x+3��
��x=1ʱ��y=-1+3=2��
��E��1��2����
��x=mʱ��y=-m+3��
��P��m��-m+3����
��y=-x2+2x+3�У���x=1ʱ��y=4��
��D��1��4��
��x=mʱ��y=-m2+2m+3��
��F��m��-m2+2m+3��
���߶�DE=4-2=2��
�߶�PF=-m2+2m+3-��-m+3��=-m2+3m
��PF��DE��
�൱PF=EDʱ���ı���PEDFΪƽ���ı��Σ�
��-m2+3m=2����ã�m1=2��m2=1���������⣬��ȥ����
��ˣ���m=2ʱ���ı���PEDFΪƽ���ı��Σ�
����ֱ��PF��x�ύ�ڵ�M����B��3��0����O��0��0�����ɵã�OB=OM+MB=3��
��S=S��BPF+S��CPF
��S= PF•BM+
PF•BM+ PF•OM=
PF•OM= PF•��BM+OM��=
PF•��BM+OM��= PF•OB��
PF•OB��
��S= ×3��-m2+3m��=-
×3��-m2+3m��=- m2+
m2+ m��0��m��3����
m��0��m��3����
������������Ҫ�����˶��κ������ۺ�Ӧ�ã����ݶ��κ����ó���ص������ͶԳ���Ľ���ʽ�ǽ���Ļ�����
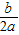 �ɵó��Գ���Ľ���ʽ��
�ɵó��Գ���Ľ���ʽ����2��PF�ij����ǵ�x=mʱ�������ߵ�ֵ��ֱ��BC����һ�κ�����ֵ�IJ���ȸ���B��C���������BC����ֱ�ߵĽ���ʽ��Ȼ��m�ֱ����ֱ��BC�������ߵĽ���ʽ�У���ó���������ֵ�IJ����PF�ij���
����ֱ��BC�Ľ���ʽ���ɵó�E������꣬���������ߵĽ���ʽ�����D������꣬Ȼ���������ϵ������ľ��빫ʽ�������DE�ij���Ȼ����PF=DE�����������ʱm��ֵ��
��3���ɽ�������BCF�ֳ�����������
һ������������PFC����PFΪ�ױߣ���P�ĺ�����Ϊ���ɵó�������PFC�������
һ������������PFB����PFΪ�ױߣ���P��B����ĺ������ľ���ֵΪ�ߣ��������������PFB�������
Ȼ�����������BCF�����=������PFC�����+������PFB����������������S��m�ĺ�����ϵʽ��
���
 �⣺��1��A��-1��0����B��3��0����C��0��3����
�⣺��1��A��-1��0����B��3��0����C��0��3���������ߵĶԳ����ǣ�ֱ��x=1��
��2������ֱ��BC�ĺ�����ϵʽΪ��y=kx+b��
��B��3��0����C��0��3���ֱ����ã�
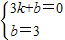
��ã�k=-1��b=3��
����ֱ��BC�ĺ�����ϵʽΪ��y=-x+3��
��x=1ʱ��y=-1+3=2��
��E��1��2����
��x=mʱ��y=-m+3��
��P��m��-m+3����
��y=-x2+2x+3�У���x=1ʱ��y=4��
��D��1��4��
��x=mʱ��y=-m2+2m+3��
��F��m��-m2+2m+3��
���߶�DE=4-2=2��
�߶�PF=-m2+2m+3-��-m+3��=-m2+3m
��PF��DE��
�൱PF=EDʱ���ı���PEDFΪƽ���ı��Σ�
��-m2+3m=2����ã�m1=2��m2=1���������⣬��ȥ����
��ˣ���m=2ʱ���ı���PEDFΪƽ���ı��Σ�
����ֱ��PF��x�ύ�ڵ�M����B��3��0����O��0��0�����ɵã�OB=OM+MB=3��
��S=S��BPF+S��CPF
��S=
 PF•BM+
PF•BM+ PF•OM=
PF•OM= PF•��BM+OM��=
PF•��BM+OM��= PF•OB��
PF•OB����S=
 ×3��-m2+3m��=-
×3��-m2+3m��=- m2+
m2+ m��0��m��3����
m��0��m��3����������������Ҫ�����˶��κ������ۺ�Ӧ�ã����ݶ��κ����ó���ص������ͶԳ���Ľ���ʽ�ǽ���Ļ�����

��ϰ��ϵ�д�
 �ظ���ʦ�㲦ϵ�д�
�ظ���ʦ�㲦ϵ�д�
�����Ŀ
 ��ͼ��������y=ax2+bx+c��a��0����x����������A��-1��0����B��3��0��������ͼ��֪y��0ʱ��x��ȡֵ��Χ�ǣ�������
��ͼ��������y=ax2+bx+c��a��0����x����������A��-1��0����B��3��0��������ͼ��֪y��0ʱ��x��ȡֵ��Χ�ǣ�������| A��-1��x��3 | B��3��x��-1 | C��x��-1��x��3 | D��x��-1��x��3 |
 26����֪����ͼ��������C1��C2����x��Գƣ�������C1��C3����y��Գƣ�������C1��C2��C3��x���ཻ��A��B��C��D�ĵ㣻��y�ཻ��E��F���㣻H��G��M�ֱ�Ϊ������C1��C2��C3�Ķ��㣮HN��ֱ��x�ᣬ����ΪN����|OE|��|HN|��|AB|��|HG|
26����֪����ͼ��������C1��C2����x��Գƣ�������C1��C3����y��Գƣ�������C1��C2��C3��x���ཻ��A��B��C��D�ĵ㣻��y�ཻ��E��F���㣻H��G��M�ֱ�Ϊ������C1��C2��C3�Ķ��㣮HN��ֱ��x�ᣬ����ΪN����|OE|��|HN|��|AB|��|HG| ��ͼ�������߽�x���ڵ�A��-2��0������B��4��0������y���ڵ�C��0��4����
��ͼ�������߽�x���ڵ�A��-2��0������B��4��0������y���ڵ�C��0��4���� ��PΪԲ�ĵ�Բ������A��������ֱ��BM���У������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
��PΪԲ�ĵ�Բ������A��������ֱ��BM���У������ڣ������P�����ꣻ�������ڣ���˵�����ɣ� ����C�ǵ�A���ڵ�B�ĶԳƵ㣬��F���߶�BC���е㣬ֱ��l����F����y��ƽ�У�ֱ��y=-x+m����C����y����D�㣮
����C�ǵ�A���ڵ�B�ĶԳƵ㣬��F���߶�BC���е㣬ֱ��l����F����y��ƽ�У�ֱ��y=-x+m����C����y����D�㣮