题目内容
把两块全等的直角三角形ABC和DEF 叠放在一起,使三角板DEF的锐角顶点D与三角板ABC的斜边中点O 重合,其中∠ABC=∠DEF=90。,∠C=∠F=45。,AB=DE=4把三角板ABC固定不动,让三角板DEF绕点O旋转,设射线DE与射线AB相交于点P,射线DF与线段BC相交于点Q。
(1)如图1,当射线DF经过点B,即点Q与点B重合时,易证△APD∽△CDQ,此时AP﹒CQ的值为( )。将三角板DEF由图1所示的位置绕点O沿逆时针方向旋转,设旋转角为α。 其中0。<α<90。 ,则 AP﹒CQ的值是否会改变?答:( )(填“会”或“不会”)此时AP﹒CQ的值为( )(不必说明理由)
(2)在(1)的条件下,设CQ=x,两块三角板重叠面积为y,求y与x的函数关系式.(图2、图3供解题用)
(3)在(1)的条件下,PQ能否与AC平行?若能,求出y的值;若不能,试说明理由。
(1)如图1,当射线DF经过点B,即点Q与点B重合时,易证△APD∽△CDQ,此时AP﹒CQ的值为( )。将三角板DEF由图1所示的位置绕点O沿逆时针方向旋转,设旋转角为α。 其中0。<α<90。 ,则 AP﹒CQ的值是否会改变?答:( )(填“会”或“不会”)此时AP﹒CQ的值为( )(不必说明理由)
(2)在(1)的条件下,设CQ=x,两块三角板重叠面积为y,求y与x的函数关系式.(图2、图3供解题用)
(3)在(1)的条件下,PQ能否与AC平行?若能,求出y的值;若不能,试说明理由。
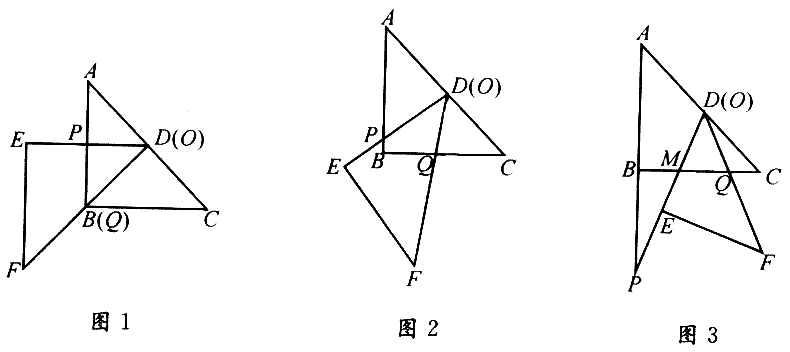
(1)8,不会,8;
(2)当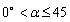 时,如图2
时,如图2
过点D作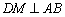 于M,
于M, 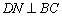 于 N
于 N
则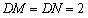
∵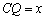 ,则
,则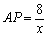
∴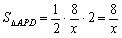
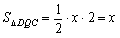
∴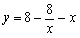
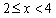
当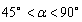 时,如图3
时,如图3
过点D作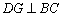 于 G,
于 G, 
∵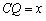 ∴
∴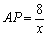
∴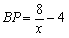
∵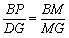 即
即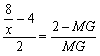
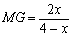
∴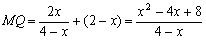
∴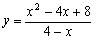 (
(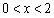 )
)
(3)在图(2)的情况下,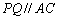 时
时
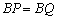 则
则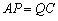
∴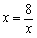 则
则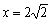
当 ,
,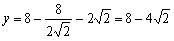
(2)当
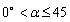 时,如图2
时,如图2过点D作
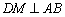 于M,
于M, 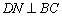 于 N
于 N则
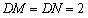
∵
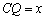 ,则
,则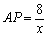
∴
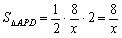
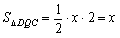
∴
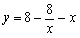
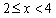
当
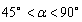 时,如图3
时,如图3过点D作
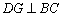 于 G,
于 G, 
∵
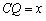 ∴
∴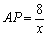
∴
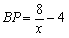
∵
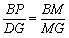 即
即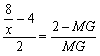
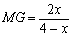
∴
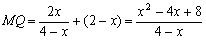
∴
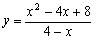 (
(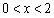 )
)(3)在图(2)的情况下,
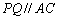 时
时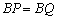 则
则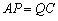
∴
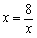 则
则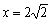
当
 ,
,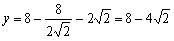

练习册系列答案
相关题目
 将两块斜边长度相等的等腰直角三角纸板如图(1)摆放,若把图(1)中的△BCN逆时针旋转90°,得到图(2),图(2)中除△ABC≌△CED、△BCN≌△ACF外,你还能找到一对全等的三角形吗?写出你的结论并说明理由.
将两块斜边长度相等的等腰直角三角纸板如图(1)摆放,若把图(1)中的△BCN逆时针旋转90°,得到图(2),图(2)中除△ABC≌△CED、△BCN≌△ACF外,你还能找到一对全等的三角形吗?写出你的结论并说明理由. 将两块斜边长度相等的等腰直角三角纸板如图(1)摆放,若把图(1)中的△BCN逆时针旋转90°,得到图(2),图(2)中除△ABC≌△CED、△BCN≌△ACF外,你还能找到一对全等的三角形吗?写出你的结论并说明理由.
将两块斜边长度相等的等腰直角三角纸板如图(1)摆放,若把图(1)中的△BCN逆时针旋转90°,得到图(2),图(2)中除△ABC≌△CED、△BCN≌△ACF外,你还能找到一对全等的三角形吗?写出你的结论并说明理由.

