题目内容
已知
、
是关于x的一元二次方程
的两个实数根，使得
成立，求其实数
的可能值。（20分）
、是关于x的一元二次方程的两个实数根，使得成立，求其实数的可能值。（20分）
试题分析：由条件知
，解得
或
．又由根与系数的关系知
，
，于是
， （10分）由
，解得
（舍去）或
． （15分）于是
．综上所述，所求的实数点评：二次函数的解析式有三种形式：（1）一般式：y=ax2+bx+c（a≠0，a、b、c为常数）；（2）顶点式：y=a（x-h）2+k；（3）交点式（与x轴）：y=a（x-x1）（x-x2）．
练习册系列答案
阅读快车系列答案
相关题目
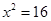的根是（ ）．
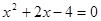的一个根，则代数式
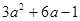的值为 .
．
=0①，
，经检验，a=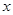
的一元二次方程
（
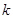为常数）．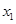
，
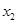为方程的两个实数根，且
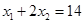，试求出方程的两个实数根和
的值是（ ）