题目内容
如图①,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为M(2,-3),且经过点A(0,1),直线y=x+1与抛物线交于A点和B点.
(1)求这条抛物线的解析式;
(2)求△ABM的面积;
(3)如图②,点P是x轴上的一动点,请探索:
①过点P作PQ∥AB,交BM于点Q,连接AQ,AP,当△APQ的面积最大时,求P的坐标.
②是否存在点P,使得△PAB是直角三角形?若存在,求出所有的点P坐标;若不存在,请说明理由.
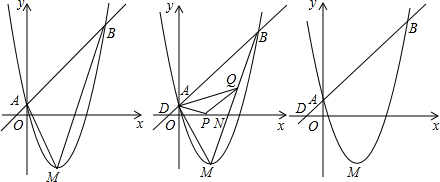
(1)求这条抛物线的解析式;
(2)求△ABM的面积;
(3)如图②,点P是x轴上的一动点,请探索:
①过点P作PQ∥AB,交BM于点Q,连接AQ,AP,当△APQ的面积最大时,求P的坐标.
②是否存在点P,使得△PAB是直角三角形?若存在,求出所有的点P坐标;若不存在,请说明理由.

分析:(1)利用顶点式求出二次函数解析式即可;
(2)首先得出D点坐标,把y=x+1代入y=(x-2)2-3,得出x的值,再利用S△ABM=S△AMN+S△BMN求出即可;
(3)①首先求出MB所在直线的解析式为:y=3x-9,进而得出△NQP∽△NBD,即可表示出QP的长,再表示出CP的长,再利用二次函数最值求法得出P点坐标;
②分三种情况讨论:Ⅰ.当∠BAP=90°,得出△DAP∽△DHB,Ⅱ.当∠APB=90°时,得出△AOP∽△PHB,Ⅲ.当∠ABP=90°时,得出△AOD∽△PBD分别求出即可.
(2)首先得出D点坐标,把y=x+1代入y=(x-2)2-3,得出x的值,再利用S△ABM=S△AMN+S△BMN求出即可;
(3)①首先求出MB所在直线的解析式为:y=3x-9,进而得出△NQP∽△NBD,即可表示出QP的长,再表示出CP的长,再利用二次函数最值求法得出P点坐标;
②分三种情况讨论:Ⅰ.当∠BAP=90°,得出△DAP∽△DHB,Ⅱ.当∠APB=90°时,得出△AOP∽△PHB,Ⅲ.当∠ABP=90°时,得出△AOD∽△PBD分别求出即可.
解答: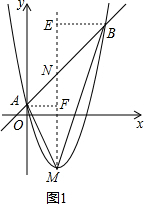 解:(1)∵抛物线y=ax2+bx+c(a≠0)的顶点坐标为M(2,-3),
解:(1)∵抛物线y=ax2+bx+c(a≠0)的顶点坐标为M(2,-3),
∴设y=a(x-2)2-3,将点A(0,1)代入得,
1=4a-3,
∴a=1
∴y=(x-2)2-3;
(2)当y=0时,0=x+1,
∴x=-1,∴D(-1,0)
把y=x+1代入y=(x-2)2-3,得
,
解得:x1=0,x2=5,
如图1,过点M作MN∥y轴交AB于点N,过点A作AF⊥MN于点F,过点B作BE⊥MN与点E,
当x=2时,y=x+1=3,
∴MN=6,
∴S△ABM=S△AMN+S△BMN=
+
=
×6×5=15;
(3)①,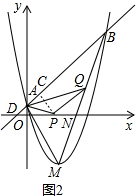
∵B(5,6),A(-1,0)
∴BD=6
设MB所在直线的解析式为y=kx+b,
把点B,点M则:
∴
,
∴MB所在直线的解析式为:y=3x-9,
∴N(3,0),
∴ND=3-(-1)=4
设P(x,0),则PN=3-x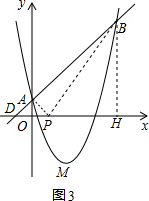
∵PQ∥AB,
∴△NQP∽△NBD,
∴
=
,
∴
=
,
∴PQ=
,
如图2,过点P作PC⊥AB于点C,
∵直线y=x+1交x轴于点(-1,0),
∴∠ADO=45°,
∴Rt△PCD为等腰Rt△,
CP=
DP=
(x+1)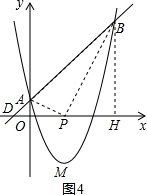 ,
,
∴△APQ的面积=
×
×
(x+1)=-
(x2-2x-3)=-
(x-1)2+3,
∴x=1时,S的值最大,
此时点P(1,0);
②分三种情况讨论:
Ⅰ.当∠BAP=90°,如图3,
∵∠DAP=∠HDB,∠BHD=∠DAP,
∴△DAP∽△DHB,
∴
=
,
∴
=
,
∴解得:DP=2,
∴OP=1,
∴P1(1,0),
Ⅱ.当∠APB=90°时,如图4,
∵∠APO+∠BPH=90°,∠APO+∠OAP=90°,
∴∠OAP=∠BPH,
∵∠AOP=∠PHB=90°,
∴△AOP∽△PHB,
∴
=
,
∴
=
,
解得:OP=2或3,
∴P2(2,0),P3(3,0),
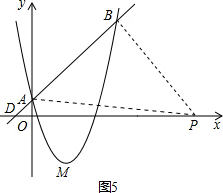
Ⅲ.当∠ABP=90°时,如图5,
∵∠BDP=∠ODA,∠DBP=∠AOD=90°,
∴△AOD∽△PBD,
∴
=
,
∴
=
,
解得:PD=12,
∴OP=11,
P4(11,0),
综上所述:P点坐标为:(1,0),(2,0),(3,0),(11,0).
 解:(1)∵抛物线y=ax2+bx+c(a≠0)的顶点坐标为M(2,-3),
解:(1)∵抛物线y=ax2+bx+c(a≠0)的顶点坐标为M(2,-3),∴设y=a(x-2)2-3,将点A(0,1)代入得,
1=4a-3,
∴a=1
∴y=(x-2)2-3;
(2)当y=0时,0=x+1,
∴x=-1,∴D(-1,0)
把y=x+1代入y=(x-2)2-3,得
|
解得:x1=0,x2=5,
如图1,过点M作MN∥y轴交AB于点N,过点A作AF⊥MN于点F,过点B作BE⊥MN与点E,
当x=2时,y=x+1=3,
∴MN=6,
∴S△ABM=S△AMN+S△BMN=
| MN×AF |
| 2 |
| MN×BE |
| 2 |
| 1 |
| 2 |
(3)①,

∵B(5,6),A(-1,0)
∴BD=6
| 2 |
设MB所在直线的解析式为y=kx+b,
把点B,点M则:
|
∴
|
∴MB所在直线的解析式为:y=3x-9,
∴N(3,0),
∴ND=3-(-1)=4
设P(x,0),则PN=3-x

∵PQ∥AB,
∴△NQP∽△NBD,
∴
| PQ |
| BD |
| PN |
| DN |
∴
| PQ | ||
6
|
| 3-x |
| 4 |
∴PQ=
3
| ||
| 2 |
如图2,过点P作PC⊥AB于点C,
∵直线y=x+1交x轴于点(-1,0),
∴∠ADO=45°,
∴Rt△PCD为等腰Rt△,
CP=
| ||
| 2 |
| ||
| 2 |
 ,
,∴△APQ的面积=
| 1 |
| 2 |
3
| ||
| 2 |
| ||
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
∴x=1时,S的值最大,
此时点P(1,0);
②分三种情况讨论:
Ⅰ.当∠BAP=90°,如图3,
∵∠DAP=∠HDB,∠BHD=∠DAP,
∴△DAP∽△DHB,
∴
| DP |
| DB |
| DA |
| DH |
∴
| DP | ||
6
|
| ||
| 6 |
∴解得:DP=2,
∴OP=1,
∴P1(1,0),

Ⅱ.当∠APB=90°时,如图4,
∵∠APO+∠BPH=90°,∠APO+∠OAP=90°,
∴∠OAP=∠BPH,
∵∠AOP=∠PHB=90°,
∴△AOP∽△PHB,
∴
| AO |
| PH |
| PO |
| BH |
∴
| 1 |
| 5-OP |
| OP |
| 6 |
解得:OP=2或3,
∴P2(2,0),P3(3,0),
Ⅲ.当∠ABP=90°时,如图5,
∵∠BDP=∠ODA,∠DBP=∠AOD=90°,
∴△AOD∽△PBD,
∴
| OD |
| BD |
| AD |
| PD |
∴
| 1 | ||
6
|
| ||
| PD |
解得:PD=12,
∴OP=11,
P4(11,0),
综上所述:P点坐标为:(1,0),(2,0),(3,0),(11,0).
点评:此题主要考查了二次函数的综合应用以及相似三角形的判定与性质以及三角形面积和二次函数最值问题,利用分类讨论得出是解题关键.

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目




 轴上,CF交y轴于点B(0,2),且其面积为8.
轴上,CF交y轴于点B(0,2),且其面积为8.