题目内容
如图,是用棋子摆成的图案,摆第一个图案需要7枚棋子,摆第二个图案需要19枚棋子,第三个图案需要37枚棋子,按照这样的方式摆下去,则摆第六个图案需要 枚棋子,摆第n个图案需要 枚棋子.
【答案】分析:本题可依次解出n=1,2,3,…,图案需要的棋子枚数.再根据规律以此类推,可得出第6个及第n个图案需要的棋子枚数.
解答::∵n=1时,总数是6+1=7;
n=2时,总数为6×(1+2)+1=19;
n=3时,总数为6×(1+2+3)+1=37枚;
…;
∴n=6时,总数为6×(1+2+3…+6)+1=127枚;
…;
∴n=n时,有6×(1+2+3+…n)+1=6×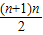 +1=3n2+3n+1枚.
+1=3n2+3n+1枚.
故答案为:127,3n2+3n+1.
点评:本题是一道找规律的题目,这类题型在中考中经常出现.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.
解答::∵n=1时,总数是6+1=7;
n=2时,总数为6×(1+2)+1=19;
n=3时,总数为6×(1+2+3)+1=37枚;
…;
∴n=6时,总数为6×(1+2+3…+6)+1=127枚;
…;
∴n=n时,有6×(1+2+3+…n)+1=6×
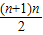 +1=3n2+3n+1枚.
+1=3n2+3n+1枚.故答案为:127,3n2+3n+1.
点评:本题是一道找规律的题目,这类题型在中考中经常出现.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
如图,是用棋子摆成的图案,按照这样的方式摆下去,则摆第n个图案需要的棋子数为( )


| A、6n+1 | B、6n+7 | C、3n2+3n-1 | D、3n2+3n+1 |
 图案需要
图案需要

