题目内容
『问题情境』勾股定理是一条古老的数学定理,它有多种证明方法,我国汉代数学家赵爽根据弦图,利用面积法进行了证明.著名数学家华罗庚曾提出把“数形关系”(勾股定理)带到其他星球,作为地球人与其它星球“人”进行第一次“谈话”的语言.
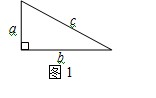
『定理表述』请你根据图1中的直角三角形叙述勾股定理(用文字及符号语言叙述).
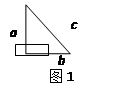
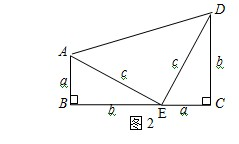
『尝试证明』以图1中的直角三角形为基础,可以构造出以a、b为底,以a+b为高的直角梯形(如图2),请你利用图2,验证勾股定理.
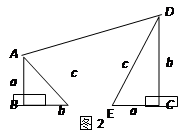
『知识拓展』利用图2中的直角梯形,我们可以证明<.其证明步骤如下:
∵BC=a+b,AD= ,
又在直角梯形ABCD中,BC AD(填大小关系),
即 .
∴<.
解:『定理表述』如果直角三角形的两直角边长分别为a,b斜边长为c,
那么![]()
![]()

![]()
![]() 『尝试证明』∵Rt△ABE≌Rt△ECD,∴∠AEB=∠EDC
『尝试证明』∵Rt△ABE≌Rt△ECD,∴∠AEB=∠EDC
又∠EDC+∠DEC=90°∴∠AEB+∠DEC=90°∴∠AED=90°
∵S![]()
![]() ∴
∴![]()
整理,得
![]()
『知识拓展』 AD=![]() ,BC<AD , ∴a+b<
,BC<AD , ∴a+b<
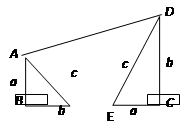
解析:略

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目

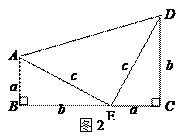

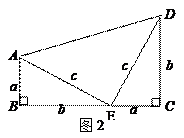


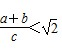 .其证明步骤如下:∵BC=a+b,AD=( ),
.其证明步骤如下:∵BC=a+b,AD=( ),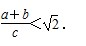 .
.