题目内容
若a、b、c是直角三角形的三条边长,斜边c上的高的长是h,给出下列结论:①以a2,b2,c2的长为边的三条线段能组成一个三角形
②以
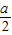 ,
,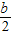 ,
,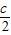 的长为边的三条线段能组成直角三角形
的长为边的三条线段能组成直角三角形③以a+b,c+h,h的长为边的三条线段能组成直角三角形
④以
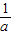 ,
,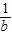 ,
,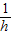 的长为边的三条线段能组成直角三角形.其中所有正确结论的序号为 .
的长为边的三条线段能组成直角三角形.其中所有正确结论的序号为 .
【答案】分析:根据勾股定理的逆定理进行逐项分析解答即可.
解答:解:①若直角三角形的三边,a= ,b=1,c=2,得a2=3,b2=1,c2=4,但3+1=4,所以a2,b2,c2的长为边的三条线段不能组成一个三角形,故本项错误;
,b=1,c=2,得a2=3,b2=1,c2=4,但3+1=4,所以a2,b2,c2的长为边的三条线段不能组成一个三角形,故本项错误;
②因为a2+b2=c2,所以(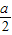 )2+(
)2+(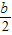 )2=(
)2=(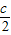 )2,故本项正确;
)2,故本项正确;
③因为(a+b)2=a2+b2+2ab=c2+2ch,(c+h)2=c2+h2+2ch,所以(a+b)2+h2=(c+h)2,能组成直角三角形,故本项正确;
④因为( )2+(
)2+(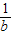 )2=(a2+b2)÷(ab)2=
)2=(a2+b2)÷(ab)2=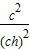 =(
=(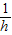 )2,所以,以
)2,所以,以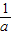 ,
, ,
,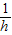 的长为边的三条线段能组成直角三角形,故本项正确.
的长为边的三条线段能组成直角三角形,故本项正确.
故答案为②③④.
点评:本题主要考查勾股定理的逆定理,三角形三边关系,关键在于熟练运用勾股定理的逆定理.
解答:解:①若直角三角形的三边,a=
 ,b=1,c=2,得a2=3,b2=1,c2=4,但3+1=4,所以a2,b2,c2的长为边的三条线段不能组成一个三角形,故本项错误;
,b=1,c=2,得a2=3,b2=1,c2=4,但3+1=4,所以a2,b2,c2的长为边的三条线段不能组成一个三角形,故本项错误;②因为a2+b2=c2,所以(
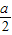 )2+(
)2+(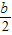 )2=(
)2=(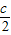 )2,故本项正确;
)2,故本项正确;③因为(a+b)2=a2+b2+2ab=c2+2ch,(c+h)2=c2+h2+2ch,所以(a+b)2+h2=(c+h)2,能组成直角三角形,故本项正确;
④因为(
 )2+(
)2+(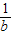 )2=(a2+b2)÷(ab)2=
)2=(a2+b2)÷(ab)2=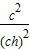 =(
=(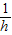 )2,所以,以
)2,所以,以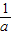 ,
, ,
,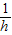 的长为边的三条线段能组成直角三角形,故本项正确.
的长为边的三条线段能组成直角三角形,故本项正确.故答案为②③④.
点评:本题主要考查勾股定理的逆定理,三角形三边关系,关键在于熟练运用勾股定理的逆定理.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
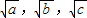 的长为边的三条线段能组成一个三角形
的长为边的三条线段能组成一个三角形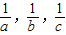 的长为边的三条线段能组成直角三角形
的长为边的三条线段能组成直角三角形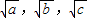 的长为边的三条线段能组成一个三角形
的长为边的三条线段能组成一个三角形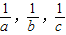 的长为边的三条线段能组成直角三角形
的长为边的三条线段能组成直角三角形