题目内容
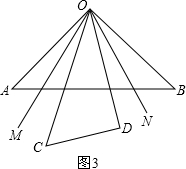
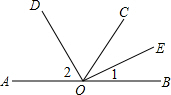
如图，AB为直线，OC是∠AOD的平分线，OE在∠BOD内，∠DOE=
∠BOD，∠COE=72°，求∠EOB．
| 1 |
| 3 |
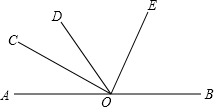
如图，设∠DOE=x，
∵∠DOE=
∠BOD，
∴∠BOE=2x，
又∵OC是∠AOD的平分线，∠COE=72°，
∴∠AOC=∠COD=72°-x；
∴2×（72°-x）+3x=180°，
解得x=36°，
∴∠BOE=2x=2×36°=72°．
∵∠DOE=
| 1 |
| 3 |
∴∠BOE=2x，
又∵OC是∠AOD的平分线，∠COE=72°，
∴∠AOC=∠COD=72°-x；
∴2×（72°-x）+3x=180°，
解得x=36°，
∴∠BOE=2x=2×36°=72°．
练习册系列答案
名校课堂系列答案
相关题目
