题目内容
要对一块长60m、宽40m的矩形荒地ABCD进行绿化和硬化.

(1)设计方案如图①所示,矩形P、Q为两块绿地,其余为硬化路面,P、Q两块绿地周围的硬化路面宽都相等,并使两块绿地面积的和为矩形ABCD面积的 ,求P、Q两块绿地周围的硬化路面的宽.
,求P、Q两块绿地周围的硬化路面的宽.
(2)某同学有如下设想:设计绿化区域为相外切的两等圆,圆心分别为O1和O2,且O1到AB,BC,AD的距离与O2到CD,BC,AD的距离都相等,其余为硬化地面,如图②所示,这个设想是否成立?若成立,求出圆的半径;若不成立,说明理由.

(1)设计方案如图①所示,矩形P、Q为两块绿地,其余为硬化路面,P、Q两块绿地周围的硬化路面宽都相等,并使两块绿地面积的和为矩形ABCD面积的
 ,求P、Q两块绿地周围的硬化路面的宽.
,求P、Q两块绿地周围的硬化路面的宽.(2)某同学有如下设想:设计绿化区域为相外切的两等圆,圆心分别为O1和O2,且O1到AB,BC,AD的距离与O2到CD,BC,AD的距离都相等,其余为硬化地面,如图②所示,这个设想是否成立?若成立,求出圆的半径;若不成立,说明理由.
(1)设P、Q两块绿地周围的硬化路面的宽都为x m,根据题意,得:
(60―3x)(40―2x)=60×40× .
.
解得x1=10,x2=30.
经检验,x2=30不符合题意,舍去.
所以,两块绿地周围的硬化路面宽都为10m.
(2)设想成立.
设圆的半径为r m,O1到AB的距离为y m,根据题意,得:
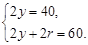
解得y=20,r=10.符合实际.
所以,设想成立,此时,圆的半径是10m.
(60―3x)(40―2x)=60×40×
 .
. 解得x1=10,x2=30.
经检验,x2=30不符合题意,舍去.
所以,两块绿地周围的硬化路面宽都为10m.
(2)设想成立.
设圆的半径为r m,O1到AB的距离为y m,根据题意,得:
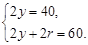
解得y=20,r=10.符合实际.
所以,设想成立,此时,圆的半径是10m.
(1)设P、Q两块绿地周围的硬化路面的宽都为x m,根据两块绿地面积的和为矩形ABCD面积的 ,即可列出方程求出结果;
,即可列出方程求出结果;
(2)设圆的半径为r m,O1到AB的距离为y m,根据O1到AB,BC,AD的距离与O2到CD,BC,AD的距离都相等,即可列出方程组求出结果。
 ,即可列出方程求出结果;
,即可列出方程求出结果;(2)设圆的半径为r m,O1到AB的距离为y m,根据O1到AB,BC,AD的距离与O2到CD,BC,AD的距离都相等,即可列出方程组求出结果。

练习册系列答案
相关题目

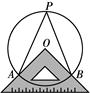
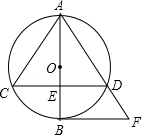
 ,求△ABC的周长.
,求△ABC的周长.
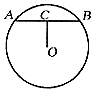
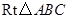 中,斜边AB=13cm,以直线BC为轴旋转一周,得到一个侧面积为65
中,斜边AB=13cm,以直线BC为轴旋转一周,得到一个侧面积为65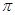
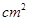 的圆锥,则BC="_______" cm.
的圆锥,则BC="_______" cm.