题目内容
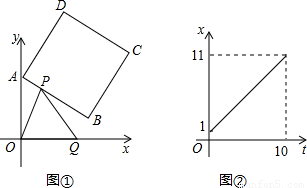
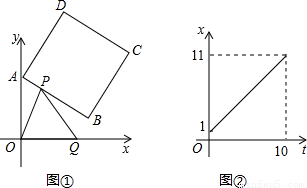
(2009•兰州)如图①,正方形ABCD中,点A、B的坐标分别为(0,10),(8,4),点C在第一象限.动点P在正方形ABCD的边上,从点A出发沿A?B?C?D匀速运动,同时动点Q以相同速度在x轴正半轴上运动,当P点到达D点时,两点同时停止运动,设运动的时间为t秒.(1)当P点在边AB上运动时,点Q的横坐标x(长度单位)关于运动时间t(秒)的函数图象如图②所示,请写出点Q开始运动时的坐标及点P运动速度;
(2)求正方形边长及顶点C的坐标;
(3)在(1)中当t为何值时,△OPQ的面积最大,并求此时P点的坐标;
(4)如果点P、Q保持原速度不变,当点P沿A?B?C?D匀速运动时,OP与PQ能否相等?若能,写出所有符合条件的t的值;若不能,请说明理由.
【答案】分析:(1)根据题意,观察图象可得x与t的关系,进而可得答案;
(2)过点B作BF⊥y轴于点F,BE⊥x轴于点E,易得BF=8,OF=BE=4,进而在Rt△AFB中,由勾股定理可得AB=10;进一步易得△ABF≌△BCH,再根据BH与OG的关系,可得C的坐标;
(3)过点P作PM⊥y轴于点M,PN⊥x轴于点N,易得△APM∽△ABF;进而可得对应边的比例关系,解可得AM、PM与t的关系,由三角形面积公式,可得答案.
(4)此题需要分类讨论:当P在BC上时,求得t的值;当P在CD上时,求得t的值;即当t=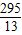 时;当P在BA上时,求得t的值.
时;当P在BA上时,求得t的值.
解答:解:(1)Q(1,0)(1分)Q的图象是一条直线,且过点(11,0).
且点P运动速度每秒钟1个单位长度.(2分)
(2)过点B作BF⊥y轴于点F,BE⊥x轴于点E,则BF=8,OF=BE=4.
∴AF=10-4=6.
在Rt△AFB中,AB=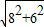 =10,(3分)
=10,(3分)
过点C作CG⊥x轴于点G,与FB的延长线交于点H.
∵∠ABC=90°,AB=BC,
∴△ABF≌△BCH.
∴BH=AF=6 CH=BF=8.
∴OG=FH=8+6=14,CG=8+4=12.
∴所求C点的坐标为(14,12).(4分)
(3)过点P作PM⊥y轴于点M,PN⊥x轴于点N,
则△APM∽△ABF.
∴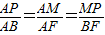 ,
,
∴ .
.
∴AM= t,PM=
t,PM= t,
t,
∴PN=OM=10- t,ON=PM=
t,ON=PM= t.
t.
设△OPQ的面积为S(平方单位),
∴S= ×(10-
×(10- t)(1+t)=5+
t)(1+t)=5+ t-
t- t2(0≤t≤10),(5分)
t2(0≤t≤10),(5分)
说明:未注明自变量的取值范围不扣分.
∵a=- ,
,
∴当t=-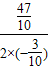 =
=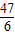 时,△OPQ的面积最大.(6分)
时,△OPQ的面积最大.(6分)
此时P的坐标为(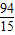 ,
,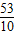 ).(7分)
).(7分)
(4)OP与PQ相等,组成等腰三角形,即当P点的横坐标等于Q点的横坐标的一半时,
当P在BC上时,8+ (t-10)=
(t-10)= (t+1),解得:t=-15(舍去)
(t+1),解得:t=-15(舍去)
当P在CD上时,14- (t-20)=
(t-20)= (t+1),解得:t=
(t+1),解得:t= ,
,
即当t= 时,OP与PQ相等.
时,OP与PQ相等.
当P在BA上时,t= ,OP与PQ相等,(9分)
,OP与PQ相等,(9分)
∴当t=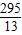 或t=
或t= 时,OP与PQ相等.
时,OP与PQ相等.
点评:本题是一道动态解析几何题,对学生的运动分析,数形结合的思想作了重点的考查,有一定的难度.
(2)过点B作BF⊥y轴于点F,BE⊥x轴于点E,易得BF=8,OF=BE=4,进而在Rt△AFB中,由勾股定理可得AB=10;进一步易得△ABF≌△BCH,再根据BH与OG的关系,可得C的坐标;
(3)过点P作PM⊥y轴于点M,PN⊥x轴于点N,易得△APM∽△ABF;进而可得对应边的比例关系,解可得AM、PM与t的关系,由三角形面积公式,可得答案.
(4)此题需要分类讨论:当P在BC上时,求得t的值;当P在CD上时,求得t的值;即当t=
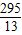 时;当P在BA上时,求得t的值.
时;当P在BA上时,求得t的值.解答:解:(1)Q(1,0)(1分)Q的图象是一条直线,且过点(11,0).
且点P运动速度每秒钟1个单位长度.(2分)
(2)过点B作BF⊥y轴于点F,BE⊥x轴于点E,则BF=8,OF=BE=4.
∴AF=10-4=6.
在Rt△AFB中,AB=
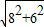 =10,(3分)
=10,(3分)过点C作CG⊥x轴于点G,与FB的延长线交于点H.

∵∠ABC=90°,AB=BC,
∴△ABF≌△BCH.
∴BH=AF=6 CH=BF=8.
∴OG=FH=8+6=14,CG=8+4=12.
∴所求C点的坐标为(14,12).(4分)
(3)过点P作PM⊥y轴于点M,PN⊥x轴于点N,
则△APM∽△ABF.
∴
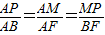 ,
,∴
 .
.∴AM=
 t,PM=
t,PM= t,
t,∴PN=OM=10-
 t,ON=PM=
t,ON=PM= t.
t.设△OPQ的面积为S(平方单位),
∴S=
 ×(10-
×(10- t)(1+t)=5+
t)(1+t)=5+ t-
t- t2(0≤t≤10),(5分)
t2(0≤t≤10),(5分)说明:未注明自变量的取值范围不扣分.
∵a=-
 ,
,∴当t=-
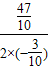 =
=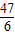 时,△OPQ的面积最大.(6分)
时,△OPQ的面积最大.(6分)此时P的坐标为(
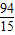 ,
,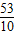 ).(7分)
).(7分)(4)OP与PQ相等,组成等腰三角形,即当P点的横坐标等于Q点的横坐标的一半时,
当P在BC上时,8+
 (t-10)=
(t-10)= (t+1),解得:t=-15(舍去)
(t+1),解得:t=-15(舍去)当P在CD上时,14-
 (t-20)=
(t-20)= (t+1),解得:t=
(t+1),解得:t= ,
,即当t=
 时,OP与PQ相等.
时,OP与PQ相等.当P在BA上时,t=
 ,OP与PQ相等,(9分)
,OP与PQ相等,(9分)∴当t=
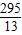 或t=
或t= 时,OP与PQ相等.
时,OP与PQ相等.点评:本题是一道动态解析几何题,对学生的运动分析,数形结合的思想作了重点的考查,有一定的难度.

练习册系列答案
相关题目
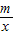 的图象的两个交点.
的图象的两个交点.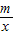 =0的解(请直接写出答案);
=0的解(请直接写出答案);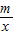 <0的解集(请直接写出答案).
<0的解集(请直接写出答案).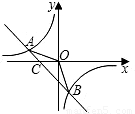
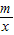 的图象的两个交点.
的图象的两个交点.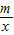 =0的解(请直接写出答案);
=0的解(请直接写出答案);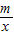 <0的解集(请直接写出答案).
<0的解集(请直接写出答案).