题目内容
如图,将△ABC沿BC方向平移得到△A′B′C′.已知BC=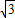 cm,△ABC与△A′B′C′重叠部分(图中阴影部分)的面积是△ABC的
cm,△ABC与△A′B′C′重叠部分(图中阴影部分)的面积是△ABC的 ,则△ABC平移的距离BB′是 cm.
,则△ABC平移的距离BB′是 cm.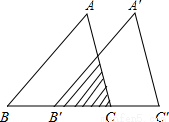
【答案】分析:设AC与A′B′相交于点D,根据平移的性质判定△ABC与△B′CD相似,然后根据相似三角形面积的比等于相似比的平方求出B′C的长度,再根据BB′=BC-B′C,计算即可得解.
解答: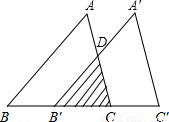 解:如图,设AC与A′B′相交于点D,
解:如图,设AC与A′B′相交于点D,
根据平移的性质,AB∥A′B′,
∴△DB′C∽△ABC,
∵重叠部分(图中阴影部分)的面积是△ABC的 ,
,
∴(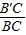 )2=
)2= ,
,
∵BC=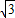 cm,
cm,
∴(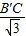 )2=
)2= ,
,
解得B′C=1,
∴BB′=BC-B′C=(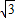 -1)cm.
-1)cm.
故答案为:(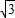 -1).
-1).
点评:本题考查了平移的性质,相似三角形的判定与性质,判定出两三角形相似,利用相似三角形面积的比等于相似比的平方求出B′C的长度是解题的关键.
解答:
 解:如图,设AC与A′B′相交于点D,
解:如图,设AC与A′B′相交于点D,根据平移的性质,AB∥A′B′,
∴△DB′C∽△ABC,
∵重叠部分(图中阴影部分)的面积是△ABC的
 ,
,∴(
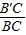 )2=
)2= ,
,∵BC=
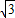 cm,
cm,∴(
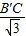 )2=
)2= ,
,解得B′C=1,
∴BB′=BC-B′C=(
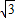 -1)cm.
-1)cm.故答案为:(
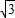 -1).
-1).点评:本题考查了平移的性质,相似三角形的判定与性质,判定出两三角形相似,利用相似三角形面积的比等于相似比的平方求出B′C的长度是解题的关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
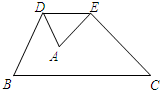 如图,将△ABC沿DE翻折,折痕DE∥BC,若
如图,将△ABC沿DE翻折,折痕DE∥BC,若| AD |
| BD |
| 1 |
| 2 |
| A、1.8 | B、2 | C、2.5 | D、3 |
 如图,将△ABC沿DE折叠,使点A与BC边的中点F重合,下列结论正确的有( )
如图,将△ABC沿DE折叠,使点A与BC边的中点F重合,下列结论正确的有( ) (2009•雅安)如图,将△ABC沿BC方向平移得到△A′B′C′.已知BC=
(2009•雅安)如图,将△ABC沿BC方向平移得到△A′B′C′.已知BC=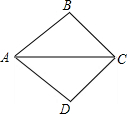 如图,将△ABC沿AC所在的直线翻折得到△ADC,且顶点B的对应顶点是D,则下列结论正确的是( )
如图,将△ABC沿AC所在的直线翻折得到△ADC,且顶点B的对应顶点是D,则下列结论正确的是( ) 如图,将△ABC沿BC方向平移1个单位得到△DEF,若△ABC的周长等于8,则四边形ABFD的周长等于( )
如图,将△ABC沿BC方向平移1个单位得到△DEF,若△ABC的周长等于8,则四边形ABFD的周长等于( )