题目内容
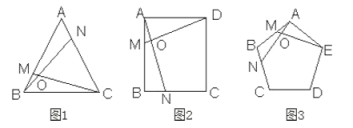
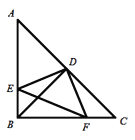
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点D是AC的中点,直角
,点D是AC的中点,直角![]() 的两边分别交AB、BC于点E、F,给出以下结论:①
的两边分别交AB、BC于点E、F,给出以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() 是等腰直角三角形. 当
是等腰直角三角形. 当![]() 在
在![]() 内绕顶点D旋转时(点E不与点A、B重合),上述结论始终成立的有____________个.
内绕顶点D旋转时(点E不与点A、B重合),上述结论始终成立的有____________个.
【答案】4
【解析】
由ED垂直于FD,BD垂直于AC,利用同角的余角相等得到一对角相等,再由三角形ABC为等腰直角三角形得到BD=CD,且∠EBD=∠C=45°,利用ASA得到三角形BED与三角形CFD全等,利用全等三角形的对应边相等,对应角相等即可做出判断.
∵ED⊥FD,BD⊥AC,
∴∠BDE+∠BDF=90°,∠BDF+∠FDC=90°,
∴∠BDE=∠FDC,
∵B、E、D、F四点共圆,
∴∠BFE=∠BDE,
∴∠BFE=∠CDF,选项④正确;
∵△ABC为等腰直角三角形,BD⊥AC,
∴∠EBD=∠C=45°,BD=CD,
在△BED和△CFD中,
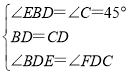 ,
,
∴△BED≌△CFD(ASA),
∴BE=CF,
∴AE=BF,选项①正确;
DE=DF,
∴△DEF为等腰直角三角形,选项⑤正确;
∴S四边形BEDF=S△BED+S△BDF=S△CFD+S△BDF=S△BDC=![]() S△ABC,选项②正确.
S△ABC,选项②正确.
∵BD是定值,EF随DF的变化而变化,只有当DF⊥BC时,EF=BD,
∴③不正确,
∴上述结论中始终成立的有4个.
故答案为:4.

练习册系列答案
相关题目