题目内容
 有一块长4米,宽3米的矩形土地,现在在矩形土地上开辟一个最大的菱形花圃.则花如图,用12米长的木方,做一个有一条横档的矩形窗子,为使透进的光线最多,选择窗子的长、宽各为
有一块长4米,宽3米的矩形土地,现在在矩形土地上开辟一个最大的菱形花圃.则花如图,用12米长的木方,做一个有一条横档的矩形窗子,为使透进的光线最多,选择窗子的长、宽各为分析:由于光线最多就是面积最大,可设长为x米,则宽为(12-3x)÷2=6-
x,表示出面积,运用函数性质求解.
| 3 |
| 2 |
解答:解:设长为x米,面积为s米2,根据题意并结合图形得S=x(6-
x)=-
x2+6x,
∵-
<0,∴S有最大值,
当x=-
=2时,S最大,此时6-
x=3,
即窗子的长为2米,高为3米时,透进的光线最多.
故答案为:2、3.
| 3 |
| 2 |
| 3 |
| 2 |
∵-
| 3 |
| 2 |
当x=-
| 6 | ||
2×(-
|
| 3 |
| 2 |
即窗子的长为2米,高为3米时,透进的光线最多.
故答案为:2、3.
点评:此题的关键是理解光线最多就是窗子面积最大时,据此求面积表达式,运用函数性质求解.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
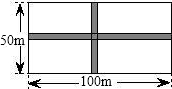 某果农有一块长100米,宽50米的矩形果园.为了摘果方便,准备沿平行于两边的方向纵、横各开一条等宽的小道.要使小道的占地面积不超过矩形果园总面积的5%,小道的宽应不超过多少米?(精确到0.1米,参考数据:
某果农有一块长100米,宽50米的矩形果园.为了摘果方便,准备沿平行于两边的方向纵、横各开一条等宽的小道.要使小道的占地面积不超过矩形果园总面积的5%,小道的宽应不超过多少米?(精确到0.1米,参考数据: 我校生物兴趣小组的同学有一块长18米、宽12米的矩形试验园.为了便于同学们参观,现要开辟一横两纵三条等宽的小路.要使种植面积为176平方米,小路应该多宽?
我校生物兴趣小组的同学有一块长18米、宽12米的矩形试验园.为了便于同学们参观,现要开辟一横两纵三条等宽的小路.要使种植面积为176平方米,小路应该多宽? 如图所示,有一块长32米,宽20米的矩形稻田ABCD,稻田内有两条处处等宽的弯曲小路,已知种植面积为540m2,求道路的宽是多少?
如图所示,有一块长32米,宽20米的矩形稻田ABCD,稻田内有两条处处等宽的弯曲小路,已知种植面积为540m2,求道路的宽是多少? 如图,有一块长35米、宽26米的矩形花草地,在上面修两条同样宽的互相垂直的小路,要使花草地的面积为850米2,问小路的宽应为多少米?
如图,有一块长35米、宽26米的矩形花草地,在上面修两条同样宽的互相垂直的小路,要使花草地的面积为850米2,问小路的宽应为多少米?