题目内容
 11、一次测试九年级若干名学生1分钟跳绳次数的频数分布直方图如图.请根据这个直方图回答下面的问题:
11、一次测试九年级若干名学生1分钟跳绳次数的频数分布直方图如图.请根据这个直方图回答下面的问题:(1)求参加测试的总人数,以及自左至右最后一组的频率;
(2)若图中自左至右各组的跳绳平均次数分别为:137次,146次,156次,164次,177次.小丽按以下方法计算参加测试学生跳绳次数的平均数是:(137+146+156+164+177)÷5=156.请你判断小丽的算式是否正确,若不正确,写出正确的算式(只列式不计算);
(3)如果测试所得数据的中位数是160次,那么测试次数为160次的学生至少有多少人?
分析:(1)从图中知,总人数为4+6+8+12+20=50人,
(2)利用加权平均数的概念可知,小丽的算法是错误的,
(3)中位数是第25和26的平均数.
(2)利用加权平均数的概念可知,小丽的算法是错误的,
(3)中位数是第25和26的平均数.
解答:解:(1)从图中可知,总人数为4+6+8+12+20=50人
自左至右最后一组的频率=12÷50=0.24;
(2)不正确.
正确的算法:(137×4+146×6+156×8+164×20+177×12)÷50;
(3)∵组距为10,
∴第四组前一个边界值为160,
又∵第一、二、三组的频数和为18,
∴50÷2-18+1=8,即次数为160次的学生至少有8人.
自左至右最后一组的频率=12÷50=0.24;
(2)不正确.
正确的算法:(137×4+146×6+156×8+164×20+177×12)÷50;
(3)∵组距为10,
∴第四组前一个边界值为160,
又∵第一、二、三组的频数和为18,
∴50÷2-18+1=8,即次数为160次的学生至少有8人.
点评:本题考查读频数分布直方图的能力和利用统计图获取信息的能力.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
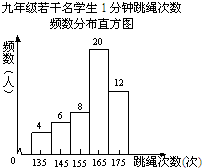 21、一次测试九年级若干名学生1分钟跳绳次数的频数分布直方图如图.请根据这个直方图回答下面的问题:
21、一次测试九年级若干名学生1分钟跳绳次数的频数分布直方图如图.请根据这个直方图回答下面的问题: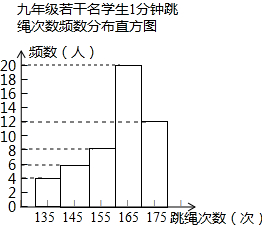 请根据这个直方图回答下面的问题:
请根据这个直方图回答下面的问题:
