题目内容
【题目】如图,矩形ABCD的对角线AC,BD相交于点O,点E,F,M,N分别为OA,OB,OC,OD的中点,连接EF,FM,MN,NE. 
(1)依题意,补全图形;
(2)求证:四边形EFMN是矩形;
(3)连接DM,若DM⊥AC于点M,ON=3,求矩形ABCD的面积.
【答案】
(1)解:如图所示:
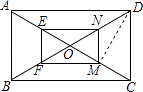
(2)证明:∵点E,F分别为OA,OB的中点,
∴EF∥AB,EF= ![]() AB,
AB,
同理:NM∥CD,MN= ![]() DC,
DC,
∵四边形ABCD是矩形,
∴AB∥DC,AB=DC,AC=BD,
∴EF∥NM,EF=MN,
∴四边形EFMN是平行四边形,
∵点E,F,M,N分别为OA,OB,OC,OD的中点,
∴EO= ![]() AO,MO=
AO,MO= ![]() CO,
CO,
在矩形ABCD中,AO=CO= ![]() AC,BO=DO=
AC,BO=DO= ![]() BD,
BD,
∴EM=EO+MO= ![]() AC,
AC,
同理可证FN= ![]() BD,
BD,
∴EM=FN,
∴四边形EFMN是矩形
(3)解:∵DM⊥AC于点M,
由(2)MO= ![]() CO,
CO,
∴DO=CD,
在矩形ABCD中,
AO=CO= ![]() AC,BO=DO=
AC,BO=DO= ![]() BD,AC=BD,
BD,AC=BD,
∴AO=BO=CO=DO,
∴△COD是等边三角形,
∴∠ODC=60°,
∵MN∥DC,
∴∠FNM=∠ODC=60°,
在矩形EFMN中,∠FMN=90°.
∴∠NFM=90°﹣∠FNM=30°,
∵NO=3,
∴FN=2NO=6,FM=3 ![]() ,MN=3,
,MN=3,
∵点F,M分别为OB,OC的中点,
∴BC=2FM=6 ![]() ,
,
∴矩形的面积为BCCD=36 ![]()
【解析】(1)根据题目要求画出图形即可;(2)根据三角形中位线定理可得EF∥AB,EF= ![]() AB,NM∥CD,MN=
AB,NM∥CD,MN= ![]() DC,再由矩形的性质可得AB∥DC,AB=DC,AC=BD,进而可得四边形EFMN是矩形;(3)根据条件可得DM垂直平分OC,进而可得DO=CO,然后证明△COD是等边三角形,进而得出BC,CD的长,进而得出答案.
DC,再由矩形的性质可得AB∥DC,AB=DC,AC=BD,进而可得四边形EFMN是矩形;(3)根据条件可得DM垂直平分OC,进而可得DO=CO,然后证明△COD是等边三角形,进而得出BC,CD的长,进而得出答案.

 阅读快车系列答案
阅读快车系列答案