Question

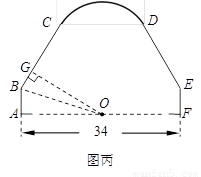
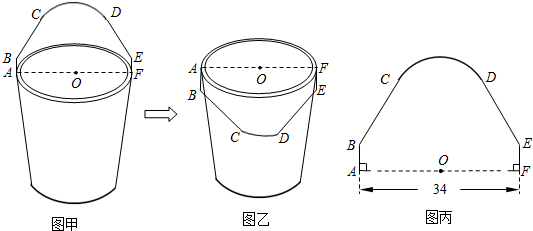
图甲是一个水桶模型示意图，水桶提手结构的平面图是轴对称图形.当点O到BC（或DE）的距离大于或等于⊙O的半径时（⊙O是桶口所在圆，半径为OA），提手才能从图甲的位置转到图乙的位置，这样的提手才合格.现用金属材料做了一个水桶提手（如图丙A-B-C-D-E-F，C-D是，其余是线段），O是AF的中点，桶口直径AF =34cm，AB=FE=5cm，∠ABC =∠FED =149°.请通过计算判断这个水桶提手是否合格.

（参考数据：≈17.72，tan73.6°≈3.40，sin75.4°≈0.97.）

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Answer 1

【答案】

解法一

连接OB，过点O作OG⊥BC于点G.         ………………1分

在Rt△ABO中，AB=5，AO=17，

∴ tan∠ABO=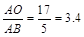，  ∴∠ABO=73.6°，………………3分

∴∠GBO=∠ABC－∠ABO=149°－73.6°=75.4°.    ………………4分

又 ∵，             ………………5分

∴在Rt△OBG中，

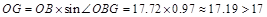.        ……………7分

∴水桶提手合格.                                ……………8分

    解法二：连接OB，过点O作OG⊥BC于点G.    ……………1分

在Rt△ABO中，AB=5，AO=17，

  ∴ tan∠ABO=，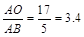                 

 ∴∠ABO=73.6°.                          ………………3分

要使OG≥OA，只需∠OBC≥∠ABO，

∵∠OBC=∠ABC－∠ABO=149°－73.6°=75.4°＞73.6°，……7分

∴水桶提手合格.                         ………………8分

 

 

 

 

 

 

 

 

【解析】略