题目内容
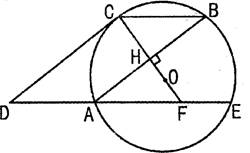
已知:如图,圆O的弦AB的延长线和切线EP相交于点P,E为切点,∠APE的平分线分别和AE,BE交于点C,D.
求证:PE·AC=PA·EC.
答案:
解析:
解析:
|
证明:因为PE切圆O于E,所以∠PED=∠A, 因为PC平分∠APE,所以∠EPD=∠APC,∠PED+∠EPD=∠A+∠APC, 因为∠EDC=∠PED+∠EPD,∠ECD=∠A+∠APC,所以∠EDC=∠ECD,ED=EC. 因为△PED∽△PAC,所以 因为ED=EC,所以PE·AC=PA·EC.
|

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
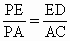 ,即PE·AC=PA·ED,
,即PE·AC=PA·ED,
 已知:如图,圆O的半径OC垂直于弦AB,点P在OC的延长线上,AC平分∠PAB.
已知:如图,圆O的半径OC垂直于弦AB,点P在OC的延长线上,AC平分∠PAB.