题目内容
 如图,AD、BE分别是等边△ABC中BC、AC上的高.M、N分别在AD、BE的延长线上,∠CBM=∠ACN.求证:AM=BN.
如图,AD、BE分别是等边△ABC中BC、AC上的高.M、N分别在AD、BE的延长线上,∠CBM=∠ACN.求证:AM=BN.
证明:在等边△ABC中,∠ABC=∠ACB=60°,AB=BC,
∵∠CBM=∠ACN,
∴∠ABC+∠CBM=∠ACB+∠ACN,
即∠ABM=∠BCN,
∵AD、BE分别是边BC、AC上的高,
∴∠BAM=∠CAN=30°,
在△ABM和△BCN中,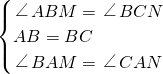 ,
,
∴△ABM≌△BCN(ASA),
∴AM=BN.
分析:根据等边三角形的性质可得∠ABC=∠ACB=60°,AB=BC,然后求出∠ABM=∠BCN,再根据等腰三角形三线合一的性质求出∠BAM=∠CAN=30°,然后利用“角边角”证明△ABM和△BCN全等,再根据全等三角形对应边相等证明即可.
点评:本题考查了全等三角形的判定与性质,等边三角形的性质,证明边相等,通常利用边所在的三角形全等进行证明,是常用的方法,要熟练掌握并灵活运用.
∵∠CBM=∠ACN,
∴∠ABC+∠CBM=∠ACB+∠ACN,
即∠ABM=∠BCN,
∵AD、BE分别是边BC、AC上的高,
∴∠BAM=∠CAN=30°,
在△ABM和△BCN中,
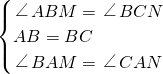 ,
,∴△ABM≌△BCN(ASA),
∴AM=BN.
分析:根据等边三角形的性质可得∠ABC=∠ACB=60°,AB=BC,然后求出∠ABM=∠BCN,再根据等腰三角形三线合一的性质求出∠BAM=∠CAN=30°,然后利用“角边角”证明△ABM和△BCN全等,再根据全等三角形对应边相等证明即可.
点评:本题考查了全等三角形的判定与性质,等边三角形的性质,证明边相等,通常利用边所在的三角形全等进行证明,是常用的方法,要熟练掌握并灵活运用.

练习册系列答案
相关题目
 如图,AD和BE把△ABC分成三个三角形和一个四边形,其中△OAE、△OAB、△OBD的面积分别为10、20、16,则四边形ODCE的面积是
如图,AD和BE把△ABC分成三个三角形和一个四边形,其中△OAE、△OAB、△OBD的面积分别为10、20、16,则四边形ODCE的面积是 4、如图,AD=DE=BE,那么图中有
4、如图,AD=DE=BE,那么图中有 如图,AD、BE分别是等边△ABC中BC、AC上的高.M、N分别在AD、BE的延长线上,∠CBM=∠ACN.求证:AM=BN.
如图,AD、BE分别是等边△ABC中BC、AC上的高.M、N分别在AD、BE的延长线上,∠CBM=∠ACN.求证:AM=BN.