题目内容
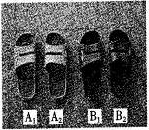 (2012•江西)如图,大小、质地相同,仅颜色不同的两双拖鞋(分左、右脚)共四只,放置在地板上[可表示为(A1,A2),(B1,B2)].
(2012•江西)如图,大小、质地相同,仅颜色不同的两双拖鞋(分左、右脚)共四只,放置在地板上[可表示为(A1,A2),(B1,B2)].(1)若先将两只左脚拖鞋中取出一只,再从两只右脚拖鞋中随机取出一只,求恰好匹配成相同颜色的一双拖鞋的概率;
(2)若从这四只拖鞋中随机的取出两只,利用树形(状)图或表格列举出所有可能出现的结果,并求恰好匹配成相同颜色的一双拖鞋的概率.
分析:(1)由若先将两只左脚拖鞋中取出一只,再从两只右脚拖鞋中随机取出一只,有A1A2,A1B2,B1B2,B1A2四种情况,恰好匹配的有A1A2,B1B2两种情况,利用概率公式即可求得答案;
(2)首先根据题意画出树形图或列出表格,即可求得所有可能的结果与恰好匹配成相同颜色的一双拖鞋的情况,然后利用概率公式求解即可求得答案.
(2)首先根据题意画出树形图或列出表格,即可求得所有可能的结果与恰好匹配成相同颜色的一双拖鞋的情况,然后利用概率公式求解即可求得答案.
解答:解:(1)∵若先将两只左脚拖鞋中取出一只,再从两只右脚拖鞋中随机取出一只,有A1A2,A1B2,B1B2,B1A2四种情况,恰好匹配的有A1A2,B1B2两种情况;
∴P(恰好匹配)=
=
…2分
(2)方法一:画树形图如下:
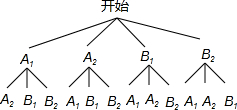
∵所有可能的结果为A1A2,A1B1,A1B2;A2A1,A2B1,A2B2;B1A1,B1A2,B1B2;B2A1,B2A2,B2B1…4分
∴从这四只拖鞋中随机的取出两只,共有12种不同的情况,其中恰好匹配的有4种,分别是A1A2,A2A1,B1B2,B2B1.
∴P(恰好匹配)=
=
.…6分
方法二:列表格如下:
可见,从这四只拖鞋中随机的取出两只,共有12种不同的情况;
其中恰好匹配的有4种,分别是A1A2,A2A1,B1B2,B2B1.
∴P(恰好匹配)=
=
.…6分
∴P(恰好匹配)=
| 2 |
| 4 |
| 1 |
| 2 |
(2)方法一:画树形图如下:

∵所有可能的结果为A1A2,A1B1,A1B2;A2A1,A2B1,A2B2;B1A1,B1A2,B1B2;B2A1,B2A2,B2B1…4分
∴从这四只拖鞋中随机的取出两只,共有12种不同的情况,其中恰好匹配的有4种,分别是A1A2,A2A1,B1B2,B2B1.
∴P(恰好匹配)=
| 4 |
| 12 |
| 1 |
| 3 |
方法二:列表格如下:
| A1B2 | A2B2 | B1B2 | - |
| A1B1 | A2B1 | - | B2B1 |
| A1A2 | - | B1A2 | B2A2 |
| - | A2A1 | B1A1 | B2A1 |
其中恰好匹配的有4种,分别是A1A2,A2A1,B1B2,B2B1.
∴P(恰好匹配)=
| 4 |
| 12 |
| 1 |
| 3 |
点评:此题考查了列表法与树状图法求概率的知识.注意列表法与树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
 (2012•江西)如图,AC经过⊙O的圆心O,AB与⊙O相切于点B,若∠A=50°,则∠C=
(2012•江西)如图,AC经过⊙O的圆心O,AB与⊙O相切于点B,若∠A=50°,则∠C= (2012•江西) 如图,已知正五边形ABCDE,请用无刻度的直尺,准确地画出它的一条对称轴(保留作图痕迹).
(2012•江西) 如图,已知正五边形ABCDE,请用无刻度的直尺,准确地画出它的一条对称轴(保留作图痕迹).
 (2012•江西)如图,等腰梯形ABCD放置在平面直角坐标系中,已知A(-2,0)、B(6,0)、D(0,3),反比例函数的图象经过点C.
(2012•江西)如图,等腰梯形ABCD放置在平面直角坐标系中,已知A(-2,0)、B(6,0)、D(0,3),反比例函数的图象经过点C. (2012•江西)如图,已知二次函数L1:y=x2-4x+3与x轴交于A、B两点(点A在点B的左边),与y轴交于点C.
(2012•江西)如图,已知二次函数L1:y=x2-4x+3与x轴交于A、B两点(点A在点B的左边),与y轴交于点C.