题目内容
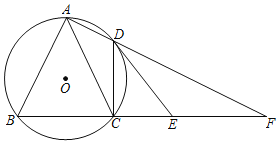
【题目】如图,四边形ABCD内接于⊙O,∠BAD=90°,AD、BC的延长线交于点F,点E在CF上,且∠DEC=∠BAC.
(1)求证:DE是⊙O的切线;
(2)当AB=AC时,若CE=4,EF=6,求⊙O的半径.
【答案】(1)DE是⊙O的切线(2)![]()
【解析】
(1)先判断出BD是圆O的直径,再判断出BD⊥DE,即可得出结论;(2)根据余角的性质和等腰三角形的性质得到∠F=∠EDF,根据等腰三角形的性质得到DE=EF=3,根据勾股定理得到CD的长,再由相似三角形的性质即可得到结论.
(1)如图,连接BD,
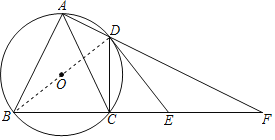
∵∠BAD=90°,
∴点O必在BD上,即:BD是直径,
∴∠BCD=90°,
∴∠DEC+∠CDE=90°,
∵∠DEC=∠BAC,
∴∠BAC+∠CDE=90°,
∵∠BAC=∠BDC,
∴∠BDC+∠CDE=90°,
∴∠BDE=90°,即:BD⊥DE,
∵点D在⊙O上,
∴DE是⊙O的切线;
(2)∵∠BAF=∠BDE=90°,
∴∠F+∠ABC=∠FDE+∠ADB=90°,
∵AB=AC,
∴∠ABC=∠ACB,
∵∠ADB=∠ACB,
∴∠F=∠EDF,
∴DE=EF=6,
∵CE=4,∠BCD=90°,
∴∠DCE=90°,
∴CD=![]() ,
,
∵∠BDE=90°,CD⊥BE,
∴△CDE∽△CBD,
∴![]() ,
,
∴BD![]() ,
,
∴⊙O的半径=![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目