题目内容
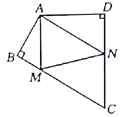
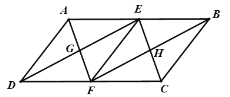
【题目】如图，平行四边形ABCD中，E、F分别为边AB、DC的中点，则图中共有平行四边形的个数是（ ）．
A.3个B.4个C.5个D.6个
【答案】D
【解析】
由在ABCD中，E、F分别为边AB、DC的中点，易得四边形ADFE、四边形AFCE、四边形BCFE、四边形BFDE是平行四边形，进而得出DE∥BF，GE=HF，则四边形GFHE为平行四边形，加上四边形ABCD为平行四边形，则图中共有6个平行四边形．
∵四边形ABCD是平行四边形，
∴AB∥CD，AB=CD，
∵E、F分别为边AB、DC的中点，
∴AE=BE=DF=CF，
∴四边形ADFE、四边形AFCE、四边形BCFE、四边形BFDE是平行四边形，
∴DE=BF，DE∥BF，
∴GE=HF，
∴四边形GFHE为平行四边形，
∵四边形ABCD为平行四边形，
∴图中共有6个平行四边形．
故答案为：D．
练习册系列答案
相关题目
【题目】为了了解学生学习的环境（教室），研究人员对某校一间（坐满学生、门窗关闭）教室中的
的总量进行检测，得到的部分数据如下：
教室连续使用时间 |
|
|
|
|
|
|
|
|
|
|
|
经研究发现，该教室空气中总量
是教室连使用时间
的一次函数．
（1）请直接写出
与的函数关系式；
（2）根据有关资料推算，当该教室空气中总量达到
时，学生将会稍感不适，则该教室连续使用__________
学生将会开始稍感不适．
（3）如果该教室在连续使用
分钟时开门通风，在学生全部离开教室的情况下，
分钟可将教室空气中的总量减少到
，求开门通风时教室空气中平均每分钟减少多少立方米？