��Ŀ����
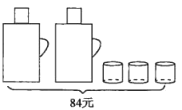
����Ŀ��ij��Ʒ�Ľ���Ϊÿ��40Ԫ���ۼ۲�����50Ԫ������ۼ�Ϊÿ��50Ԫ��ÿ���¿�����210��������ۼ۳���50Ԫ��������80Ԫ��ÿ����Ʒ���ۼ�ÿ����1Ԫ����ÿ������1��������ۼ۳���80Ԫ�������Ǽۣ���ÿ��1Ԫÿ������3������ÿ����Ʒ���ۼ�ΪxԪ��ÿ�µ�������Ϊy����
��1����y��x�ĺ�����ϵʽ��д���Ա���x��ȡֵ��Χ��
��2��ÿ����Ʒ���ۼ۶�Ϊ����Ԫʱ��ÿ���¿ɻ��������������������Ƕ���Ԫ��
���𰸡�(1)��=![]() (2) 7500Ԫ
(2) 7500Ԫ
����������������1�����ۼ۳���50Ԫ��������80Ԫ��ÿ����Ʒ���ۼ�ÿ����1Ԫ����ÿ��������1����y=260-x��50��x��80��������ۼ۳���80Ԫ�������Ǽۣ���ÿ��1Ԫÿ������3����y=420-3x��80��x��140��
��2��������=���ۼ�-�ɱ������������г�������ϵʽ��������ʽ�䷽�ɶ���ʽ�����ö��κ������������ɵã�
��⣺��1����50��x��80ʱ��y=210����x��50������y=260��x��
��80��x��140ʱ��y=210����80��50����3��x��80������y=420��3x��
��y=![]() ��
��
��2����50��x��80ʱ��w=��x2+300x��10400=����x��150��2+12100��
��x��150ʱ��w��x���������
��x=80ʱ��w���=7200��
��80��x��140ʱ��w=��3x2+540x��16800=��3��x��90��2+7500��
��x=90ʱ��w���=7500��
��x=90ʱ��W�����ֵ7500Ԫ��
��ÿ����Ʒ���ۼ۶�Ϊ90Ԫʱ��ÿ���¿ɻ�����������7500Ԫ

 Сѧ�̲�ȫ��ϵ�д�
Сѧ�̲�ȫ��ϵ�д� Сѧ��ѧ������ѿڶ���ϵ�д�
Сѧ��ѧ������ѿڶ���ϵ�д�