题目内容
如图,AB是⊙O的直径,C是⊙O上一点,AC平分∠BAD;AD⊥ CD,垂足为D.
(1)求证:CD是⊙O的切线
(2)若⊙O的直径为5,CD=2.求AC的长.
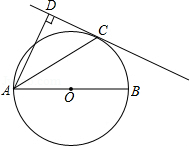
(1)求证:CD是⊙O的切线
(2)若⊙O的直径为5,CD=2.求AC的长.

(1)CD是⊙O的切线。(2)AC=2 .
.
 .
.试题分析:.解:(1)连接OC,∵AC平分∠BAD,∴∠DAC=∠BAC∵OC=OA∴∠BAC=∠ACO,又∵∠D=90°∴∠OCD=90°∴CD是⊙O的切线。
(2)连接BC.
∵AB是直径,
∴∠ACB=90°=∠ADC,
∵∠OAC=∠OCA,
∴△ADC∽△ACB,
∴
 ,AC2=5AD
,AC2=5AD在Rt△ADC中,AC2= AD2+4
∴AD2+4=5AD
∴AD=4,
∴AC=2

点评:熟知以上判定,性质,结合已知可求之,注意点;求切线时,常常连接点到圆心的线段,来证明,本题难度不大,属于基础题。

练习册系列答案
相关题目

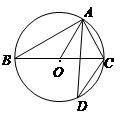



 的中点,DE垂直于AC的延长线于E,连结BC,若DE=6cm,CE=2cm,下列结论错误的是( )
的中点,DE垂直于AC的延长线于E,连结BC,若DE=6cm,CE=2cm,下列结论错误的是( )