题目内容
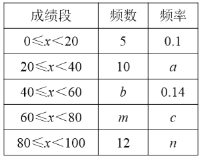
【题目】在平面直角坐标系xOy中,抛物线y=mx2﹣2mx+n(m<0)的顶点为A,与x轴交于B,C两点(点B在点C左侧),与y轴正半轴交于点D,连接AD并延长交x轴于E,连AC、DC.S△DEC:S△AEC=3:4.
(1)求点E的坐标;
(2)△AEC能否为直角三角形?若能,求出此时抛物线的函数表达式;若不能,请说明理由.

【答案】(1)E(﹣3,0);(2)二次函数解析式为:y=﹣![]() x2+
x2+![]() x+
x+![]() .
.
【解析】试题分析:(1)根据题意画出图形,再利用相似三角形的判定与性质得出EO:OF=3:1,进而得出EO的长即可得出答案;
(2)由题意可知,AE,AC不可能与x轴垂直,再得出△EFA∽△AFC,求出m的值,进而得出答案.
试题解析:解:(1)如图所示:设此抛物线对称轴与x轴交于点F,∴S△DEC:S△AEC=DO:AF=3:4.∵DO∥AF,∴△EDO∽△EAF,∴EO:EF=DO:AF=3:4,∴EO:OF=3:1,由y=mx2﹣2mx+n(m<0)得:A(1,n﹣m),D(0,n),∴OF=1,∴EO=3,∴E(﹣3,0);
(2)∵DO:AF=3:4,∴![]() =
=![]() ,∴n=﹣3m,∴y=mx2﹣2mx﹣3m=m(x2﹣2x﹣3)
,∴n=﹣3m,∴y=mx2﹣2mx﹣3m=m(x2﹣2x﹣3)
=m(x﹣3)(x+1),∴B(﹣1,0),C(3,0),A(1,﹣4m),由题意可知,AE,AC不可能与x轴垂直,∴若△AEC为直角三角形,则∠EAC=90°.又∵AF⊥EC,可得:△EFA∽△AFC,∴![]() =
=![]() ,即
,即![]() =
=![]() .∵m<0,∴m=﹣
.∵m<0,∴m=﹣![]() ,∴二次函数解析式为:y=﹣
,∴二次函数解析式为:y=﹣![]() x2+
x2+![]() x+
x+![]() .
.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案【题目】从2012年7月1日起某市执行新版居民阶梯电价,小明同学家收到了新政后的第一张电费单,小明爸爸说:“小明,请你计算一下,这个月的电费支出与新政前相比是多了还是少了?”于是小明上网了解了有关电费的收费情况,得到如下两表:
2004年1月至2012年6月执行的收费标准:
月用电量(度)50度有以下部分 | 50度有以下部分 | 超过50度但不超过200度部分 | 超过200度以上部分 |
单价(元/度) | 0.53 | 0.56 | 0.63 |
2012年7月起执行的收费标准:
月用电量(度) | 230度有以下部分 | 超过230度但不超过400度部分 | 超过400度以上部分 |
单价(元/度) | 0.53 | 0.58 | 0.83 |
(1)若小明家2012年7月份的用电量为200度,则小明家7月份的电费支出是多少元?比新政前少了多少元?
(2)若新政后小明家的月用电量为a度,请你用含a的代数式表示当月的电费支出.