题目内容
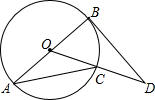 (2011•锦州)如图,AB是⊙O的直径,BD是⊙O的切线,∠D=32°,则∠A=
(2011•锦州)如图,AB是⊙O的直径,BD是⊙O的切线,∠D=32°,则∠A=29°
29°
.分析:根据切线的性质得到∠OBD=90°,再根据∠D的度数,利用三角形内角和定理求出∠BOD的度数,然后根据同弧所对的圆周角等于所对圆心角度数的一半,可得∠A=
∠BOD,由∠BOD的度数即可求出∠A的度数.
| 1 |
| 2 |
解答:解:∵BD是⊙O的切线,
∴∠OBD=90°,又∠D=32°,
∴∠BOD=180°-∠OBD-∠D=58°,
又∠BOD与∠A分别为
所对的圆心角和圆周角,
则∠A=
∠BOD=
×58°=29°.
故答案为:29°
∴∠OBD=90°,又∠D=32°,
∴∠BOD=180°-∠OBD-∠D=58°,
又∠BOD与∠A分别为
 |
| BC |
则∠A=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:29°
点评:此题考查了切线的性质,圆周角定理以及三角形的内角和定理,运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.本题利用了圆的切线垂直于过切点的直径,来构造直角三角形解决问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
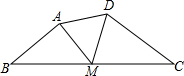 (2011•锦州)如图,四边形ABCD,M为BC边的中点.若∠B=∠AMD=∠C=45°,AB=8,CD=9,则AD的长为( )
(2011•锦州)如图,四边形ABCD,M为BC边的中点.若∠B=∠AMD=∠C=45°,AB=8,CD=9,则AD的长为( ) (2011•锦州)如图所示,在边长为1个单位的正方形网格中建立平面直角坐标系,△ABC的顶点均在格点上.
(2011•锦州)如图所示,在边长为1个单位的正方形网格中建立平面直角坐标系,△ABC的顶点均在格点上. BDO.
BDO.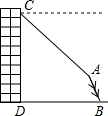 (2011•锦州)如图,小明站在窗口向外望去,发现楼下有一棵倾斜的大树,在窗口C处测得大树顶部A的俯角为45°,若已知∠ABD=60°,CD=20m,BD=16m,请你帮小明计算一下,如果大树倒在地面上,其顶端A与楼底端D的距离是多少米?(结果保留整数,参考数据:
(2011•锦州)如图,小明站在窗口向外望去,发现楼下有一棵倾斜的大树,在窗口C处测得大树顶部A的俯角为45°,若已知∠ABD=60°,CD=20m,BD=16m,请你帮小明计算一下,如果大树倒在地面上,其顶端A与楼底端D的距离是多少米?(结果保留整数,参考数据: