题目内容
(2008•济南)已知:抛物线y=ax2+bx+c(a≠0),顶点C(1,-3),与x轴交于A,B两点,A(-1,0).(1)求这条抛物线的解析式;
(2)如图,以AB为直径作圆,与抛物线交于点D,与抛物线对称轴交于点E,依次连接A,D,B,E,点P为线段AB上一个动点(P与A,B两点不重合),过点P作PM⊥AE于M,PN⊥DB于N,请判断
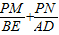 是否为定值?若是,请求出此定值;若不是,请说明理由;
是否为定值?若是,请求出此定值;若不是,请说明理由;(3)在(2)的条件下,若点S是线段EP上一点,过点S作FG⊥EP,FG分别与边AE,BE相交于点F,G(F与A,E不重合,G与E,B不重合),请判断
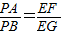 是否成立?若成立,请给出证明;若不成立,请说明理由.
是否成立?若成立,请给出证明;若不成立,请说明理由.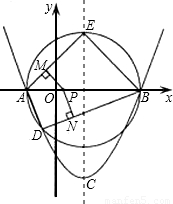
【答案】分析:(1)已知抛物线的顶点坐标就可以利用顶点式求函数的解析式.
(2)AB是圆的直径,因而∠ADB=∠AEB=90°,得到PN∥AD,得到 =
= ,同理
,同理 =
=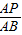 ,这样就可以求出
,这样就可以求出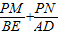 的值.
的值.
(3)易证△AEB为等腰直角三角形,过点P作PH⊥BE与H,四边形PHEM是矩形,易证△APM∽△PBH,则 ,再证明△MEP∽△EGF,则
,再证明△MEP∽△EGF,则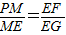 因而
因而 可证.
可证.
解答:解:(1)设抛物线的解析式为y=a(x-1)2-3(1分)
将A(-1,0)代入:0=a(-1-1)2-3,
解得a= (2分)
(2分)
所以,抛物线的解析式为y= (x-1)2-3,即y=
(x-1)2-3,即y= x2-
x2- x-
x- (3分)
(3分)
(2)是定值,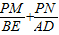 =1(4分)
=1(4分)
∵AB为直径,
∴∠AEB=90°,
∵PM⊥AE,
∴PM∥BE,
∴△APM∽△ABE,
所以 ①
①
同理: ②(5分)
②(5分)
①+②: (6分)
(6分)
(3)∵直线EC为抛物线对称轴,
∴EC垂直平分AB,
∴EA=EB,
∵∠AEB=90°,
∴△AEB为等腰直角三角形,
∴∠EAB=∠EBA=45°(7分)
如图,过点P作PH⊥BE于H,
由已知及作法可知,四边形PHEM是矩形.
∴PH=ME且PH∥ME.
在△APM和△PBH中,
∵∠AMP=∠PHB=90°,∠EAB=∠BPH=45°,
∴PH=BH,且△APM∽△PBH,
∴ ,
,
∴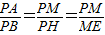 ①(8分)
①(8分)
在△MEP和△EGF中,
∵PE⊥FG,
∴∠FGE+∠SEG=90°,
∵∠MEP+∠SEG=90°,
∴∠FGE=∠MEP,
∵∠PME=∠FEG=90°,
∴△MEP∽△EGF,
∴ ②
②
由①、②知: (9分)(本题若按分类证明,只要合理,可给满分)
(9分)(本题若按分类证明,只要合理,可给满分)
点评:本题主要考查了待定系数法求二次函数的解析式,以及相似三角形的对应边的比相等.
(2)AB是圆的直径,因而∠ADB=∠AEB=90°,得到PN∥AD,得到
 =
= ,同理
,同理 =
=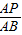 ,这样就可以求出
,这样就可以求出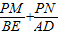 的值.
的值.(3)易证△AEB为等腰直角三角形,过点P作PH⊥BE与H,四边形PHEM是矩形,易证△APM∽△PBH,则
 ,再证明△MEP∽△EGF,则
,再证明△MEP∽△EGF,则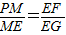 因而
因而 可证.
可证.解答:解:(1)设抛物线的解析式为y=a(x-1)2-3(1分)
将A(-1,0)代入:0=a(-1-1)2-3,
解得a=
 (2分)
(2分)所以,抛物线的解析式为y=
 (x-1)2-3,即y=
(x-1)2-3,即y= x2-
x2- x-
x- (3分)
(3分)(2)是定值,
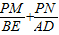 =1(4分)
=1(4分)∵AB为直径,
∴∠AEB=90°,
∵PM⊥AE,
∴PM∥BE,
∴△APM∽△ABE,
所以
 ①
①同理:
 ②(5分)
②(5分)①+②:
 (6分)
(6分)(3)∵直线EC为抛物线对称轴,
∴EC垂直平分AB,

∴EA=EB,
∵∠AEB=90°,
∴△AEB为等腰直角三角形,
∴∠EAB=∠EBA=45°(7分)
如图,过点P作PH⊥BE于H,
由已知及作法可知,四边形PHEM是矩形.
∴PH=ME且PH∥ME.
在△APM和△PBH中,
∵∠AMP=∠PHB=90°,∠EAB=∠BPH=45°,
∴PH=BH,且△APM∽△PBH,
∴
 ,
,∴
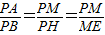 ①(8分)
①(8分)在△MEP和△EGF中,
∵PE⊥FG,
∴∠FGE+∠SEG=90°,
∵∠MEP+∠SEG=90°,
∴∠FGE=∠MEP,
∵∠PME=∠FEG=90°,
∴△MEP∽△EGF,
∴
 ②
②由①、②知:
 (9分)(本题若按分类证明,只要合理,可给满分)
(9分)(本题若按分类证明,只要合理,可给满分)点评:本题主要考查了待定系数法求二次函数的解析式,以及相似三角形的对应边的比相等.

练习册系列答案
相关题目
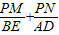 是否为定值?若是,请求出此定值;若不是,请说明理由;
是否为定值?若是,请求出此定值;若不是,请说明理由;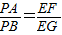 是否成立?若成立,请给出证明;若不成立,请说明理由.
是否成立?若成立,请给出证明;若不成立,请说明理由.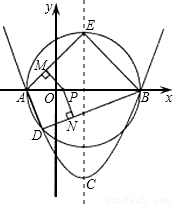
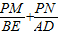 是否为定值?若是,请求出此定值;若不是,请说明理由;
是否为定值?若是,请求出此定值;若不是,请说明理由;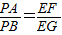 是否成立?若成立,请给出证明;若不成立,请说明理由.
是否成立?若成立,请给出证明;若不成立,请说明理由.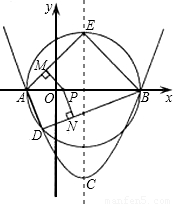
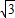 x+4
x+4 与x轴相交于点A,与直线y=
与x轴相交于点A,与直线y=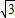 x相交于点P.
x相交于点P.
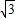 x+4
x+4 与x轴相交于点A,与直线y=
与x轴相交于点A,与直线y=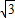 x相交于点P.
x相交于点P.