Question

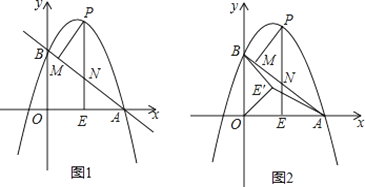
【题目】已知抛物线的顶点在轴上．

（1）若点是抛物线最低点，且落在轴正半轴上，直接写出的取值范围；

（2），是抛物线上两点，若，则；若，则，且当的绝对值为4时，为等腰直角三角形（其中）．

①求抛物线的解析式；

②设中点为，若，求点纵坐标的最小值．

Answer 1

【答案】（1）；（2）①；②当时，最小值是2．

【解析】

（1）由顶点是抛物线最低点，可判断抛物线开口向上，可判定a的符号；根据抛物线的解析式确定顶点坐标，根据顶点A落在轴正半轴上，可判定h、k的取值范围；
（2）①由已知可得当x＜0时，y随x的增大而减小，当x＞0时，y随x的增大而增大，所以对称轴为轴，即可确定抛物线为y=ax2，再由△APQ为等腰直角三角形和y1的绝对值为4，得到a=；
②设N点坐标为（x，y），PQ2=8y+4y2-（x1x2+4）2+4≥36，所以4（y+1）2≥36+（x1x2+4）2，当x1x2=-4时，y有最小值，y+1≥3，y≥2， 即N点纵坐标最小值为2．

（1）∵抛物线有最低点，
∴a＞0，
∵抛物线的顶点坐标为（h，k）在x轴正半轴上，
∴h＞0，k=0；

（2）①∵当时，；则，

∴当x＜0时，y随x的增大而减小，

当时，；则

∴当x＞0时，y随x的增大而增大，

∴抛物线的对称轴是轴，且开口向上

又顶点在轴上，所以顶点是原点

∴抛物线的解析式为，且

当是等腰直角三角形，时，，

又为顶点，所以点关于抛物线对称轴轴对称．

，

∴

设交轴于点，则，

∴点中一个坐标为，另一个为

把代入，解得

∴抛物线的解析式为

②PQ2=（x1-x2）2+（y1-y2）2≥36，
∵y1=x12，y2=x22，
∴PQ2=（x1-x2）2+（y1-y2）2

=（x1-x2）2+（x12-x22）2

=（x1-x2）2+（x12+x22）2-x12x22

=x12+x22-2x1x2+（x12+x22）2-x12x22

=4（y1+y2）+（y1+y2）2-（x12x22+8x1x2）

=4（y1+y2）+（y1+y2）2-（x12x22+8x1x2+16-16）

=4（y1+y2）+（y1+y2）2-（x1x2+4）2+4
∵设N点坐标为（x，y），N是PQ的中点，

∴ ＞0
∴2x=x1+x2，2y=y1+y2，
∴PQ2=8y+4y2-（x1x2+4）2+4≥36，
∴4（y+1）2≥36+（x1x2+4）2，

∵y+1＞0
当x1x2=-4时，y有最小值，
∴y+1≥3，
∴y≥2，
∴点N纵坐标的最小值为2