题目内容
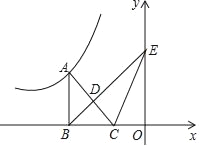
【题目】如图，已知点A在反比例函数y＝
（x＜0）上，B，C两点在x轴上，△ABC是以AC为斜边的等腰直角三角形，过点B作BD⊥AC交y轴于点E，交AC于点D，若△BCE的面积为3，则k的值为_____．
【答案】-6
【解析】
根据题意可设点A的坐标（m，n），根据等腰直角三角形的性质可得AB＝BC＝n，OB＝OE＝﹣m，再根据△BCE的面积为3，求得mn的值，从而求得k的值.
解：∵△ABC是以AC为斜边的等腰直角三角形，BD⊥AC，
∴AB＝BC，∠EBC＝45°，
∴△BOE是等腰直角三角形，
∴OB＝OE，
设A（m，n），
∴AB＝BC＝n，OB＝OE＝﹣m，
∵△BCE的面积为3，
∴
BCOE＝3，
∴OBAB＝3，
∴ （﹣m）n＝3，
∴mn＝﹣6，
∴ k＝﹣6，
故答案为﹣6．
练习册系列答案
相关题目
【题目】为了传承中华优秀传统文化，某校组织了一次八年级350名学生参加的“汉字听写”大赛，赛后发现所有参赛学生的成绩均不低于50分．为了更好地了解本次大赛的成绩分布情况，随机抽取了其中若干名学生的成绩（成绩
取整数，总分100分）作为样本进行整理，得到下列不完整的统计图表：
成绩x/分 | 频数 | 频率 |
50≤x＜60 | 2 | 0.04 |
60≤x＜70 | 6 | 0.12 |
70≤x＜80 | 9 |
|
80≤x＜90 | 0.36 | |
90≤x≤100 | 15 | 0.30 |
请根据所给信息，解答下列问题：
（1）a等于多少，b等于多少；
（2）请补全频数分布直方图；
（3）这次比赛成绩的中位数会落在哪个分数段；
（4）若成绩在90分以上（包括90分）的为“优”等，则该年级参加这次比赛的350名学生中成绩“优”等的约有多少人？
