ƒøƒ⁄»ð
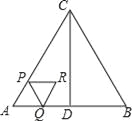
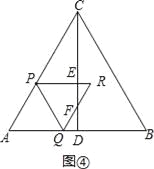
°æƒø°ø»ÁÕº£¨°˜ABC «µ»±þ»˝Ω«–Œ£¨AB=4cm£¨CD°ÕAB”⁄µ„D£¨∂ص„P¥”µ„A≥ˆ∑¢£¨—ÿAC“‘2cm/sµƒÀŸ∂»œÚ÷’µ„C‘À∂Ø£¨µ±µ„P≥ˆ∑¢∫Û£¨π˝µ„P◊˜PQ°ŒBCΩª’€œþAD©ÅDC”⁄µ„Q£¨“‘PQŒ™±þ◊˜µ»±þ»˝Ω«–ŒPQR£¨…ËÀƒ±þ–ŒAPRQ”ΰ˜ACD÷ÿµ˛≤ø∑÷Õº–Œµƒ√ʪ˝Œ™S£®cm2£©£¨µ„P‘À∂صƒ ±º‰Œ™t£®s£©£Æ
£®1£©µ±µ„Q‘⁄œþ∂ŒAD…œ ±£¨”√∫¨tµƒ¥˙ ˝ Ω±Ì æQRµƒ≥§£ª
£®2£©«Ûµ„R‘À∂صƒ¬∑≥Ã≥§£ª
£®3£©µ±µ„Q‘⁄œþ∂ŒAD…œ ±£¨«ÛS”Ît÷ƺ‰µƒ∫Ø ˝πÿœµ Ω£ª
£®4£©÷±Ω”–¥≥ˆ“‘µ„B°¢Q°¢RŒ™∂•µ„µƒ»˝Ω«–Œ «÷±Ω«»˝Ω«–Œ ±tµƒ÷µ£Æ
°æ¥∞∏°ø(1) 2t£ª(2) 2![]() +2£ª(3) µ±0£ºt°Ð
+2£ª(3) µ±0£ºt°Ð![]() ±£¨S=2
±£¨S=2![]() t2£ªµ±
t2£ªµ±![]() £ºt°Ð1 ±£¨S=-
£ºt°Ð1 ±£¨S=-![]() t2+6
t2+6![]() t-2
t-2![]() £ª(4) t=
£ª(4) t=![]() ªÚt=
ªÚt=![]()
°æΩ‚Œˆ°ø ‘Â∑÷Œˆ£∫£®1£©“◊÷§°˜APQ «µ»±þ»˝Ω«–Œ£¨º¥ø…µ√µΩQR=PQ=AP=2t£ª
£®2£©π˝µ„A◊˜AG°ÕBC”⁄µ„G£¨»ÁÕº¢⁄£¨“◊µ√µ„R‘À∂صƒ¬∑≥Ã≥§ «AG+CG£¨÷ª–Ë«Û≥ˆAG°¢CGæÕø…Ω‚æˆŒ £ª
£®3£©Àƒ±þ–ŒAPRQ”ΰ˜ACD÷ÿµ˛≤ø∑÷Õº–Œø…ƒÐ «¡‚–Œ£¨“≤ø…ƒÐ «ŒÂ±þ–Œ£¨π –Ë∑÷«ÈøˆÃ÷¬€£¨»ª∫Û‘À”√∏Ó≤π∑®æÕø…Ω‚æˆŒ £ª
£®4£©”…”⁄÷±Ω«∂•µ„≤ª»∑∂®£¨π –Ë∑÷«ÈøˆÃ÷¬€£¨÷ª–Ë∑÷°œQRB=90°„∫Õ°œRQB=90°„¡Ω÷÷«ÈøˆÃ÷¬€£¨º¥ø…Ω‚æˆŒ £Æ
‘Ã‚Ω‚Œˆ£∫£®1£©»ÁÕº¢Ÿ£¨
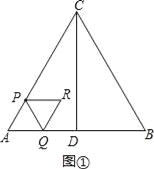
°þ°˜ABC «µ»±þ»˝Ω«–Œ£¨
°ý°œACB=°œB=60°„£Æ
°þPQ°ŒBC£¨
°ý°œAPQ=°œACB=60°„£¨°œAQP=°œB=60°„£¨
°ý°˜APQ «µ»±þ»˝Ω«–Œ£Æ
°ýPQ=AP=2t£Æ
°þ°˜PQR «µ»±þ»˝Ω«–Œ£¨
°ýQR=PQ=2t£ª
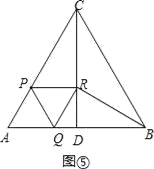
£®2£©π˝µ„A◊˜AG°ÕBC”⁄µ„G£¨»ÁÕº¢⁄£¨
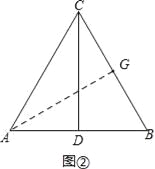
‘Úµ„R‘À∂صƒ¬∑≥Ã≥§ «AG+CG£Æ
‘⁄Rt°˜AGC÷–£¨°œAGC=90°„£¨sin60°„=![]() £¨cos60°„=
£¨cos60°„=![]() £¨AC=4£¨
£¨AC=4£¨
°ýAG=2![]() £¨CG=2£Æ
£¨CG=2£Æ
°ýµ„R‘À∂صƒ¬∑≥Ã≥§2![]() +2£ª
+2£ª
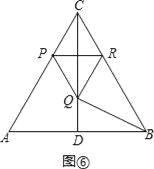
£®3£©¢Ÿµ±0£ºt°Ð![]() ±£¨»ÁÕº¢€£¨
±£¨»ÁÕº¢€£¨
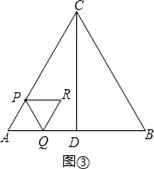
S=S¡‚–ŒAPRQ=2°¡S’˝°˜APQ=2°¡![]() °¡£®2t£©2=2
°¡£®2t£©2=2![]() t2£ª
t2£ª
¢⁄µ±![]() £ºt°Ð1 ±£¨»ÁÕº¢Ð
£ºt°Ð1 ±£¨»ÁÕº¢Ð
PE=PCsin°œPCE=£®4©Å2t£©°¡![]() =2©Åt£¨
=2©Åt£¨
°ýER=PR©ÅPE=2t©Å£®2©Åt£©=3t©Å2£¨
°ýEF=ERtanR=![]() £®3t©Å2£©
£®3t©Å2£©
°ýS=S¡‚–ŒAPRQ©ÅS°˜REF
=2![]() t2©Å
t2©Å![]() £®3t©Å2£©2=©Å
£®3t©Å2£©2=©Å![]() t2+6
t2+6![]() t©Å2
t©Å2![]() £ª
£ª
£®4£©t=![]() ªÚt=
ªÚt=![]()
÷ æ£∫¢Ÿµ±°œQRB=90°„ ±£¨»ÁÕº¢ð£¨
cos°œRQB=![]() £¨
£¨
°ýQB=2QR=2QA£¨
°ýAB=3QA=6t=4£¨
°ýt=![]() £ª
£ª
¢⁄µ±°œRQB=90°„ ±£¨»ÁÕº¢Þ£¨
Õ¨¿Ìø…µ√BC=3RC=3PC=3£®4©Å2t£©=4£¨
°ýt=![]() £Æ
£Æ

 √˚–£øŒÃ√œµ¡–¥∞∏
√˚–£øŒÃ√œµ¡–¥∞∏