题目内容
如图，半径为6的圆中，弦AB垂直平分半径OC，则弦AB的长为6
| 3 |
6
．| 3 |
分析：设AB与OC的垂足为P点，连OA，根据垂径定理，由弦AB垂直平分OC，得到PA=PB，OP=PC，而⊙O的半径OC为6cm，得OP=3，在Rt△AOP中，再根据勾股定理计算出AP，即可得到AB．
解答：
解：设AB与OC的垂足为P点，连OA，如图，
∵弦AB垂直平分OC，
∴PA=PB，OP=PC，
而⊙O的半径OC为6cm，
∴OP=3，而OA=6，
∴AP=
=3
，
∴AB=2AP=6
cm．
故答案为6
．
解：设AB与OC的垂足为P点，连OA，如图，∵弦AB垂直平分OC，
∴PA=PB，OP=PC，
而⊙O的半径OC为6cm，
∴OP=3，而OA=6，
∴AP=
| 62-32 |
| 3 |
∴AB=2AP=6
| 3 |
故答案为6
| 3 |
点评：本题考查了垂径定理：垂直于弦的直径平分弦，并且平分弦所对的弧．也考查了勾股定理．
练习册系列答案
相关题目
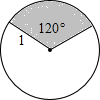如图，半径为1的圆中，圆心角为120°的扇形面积为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
如图，半径为10的圆中，弦AB垂直平分半径OC，则弦AB的长为（ ）
（B）
（C）
（D） 