题目内容
解答题.解答应写出文字说明、证明过程或演算步骤
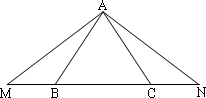
如图,⊿ABC,AB=AC,点M、N分别在BC所在直线上,且AM=AN.
求证:BM=CN
答案:
解析:
解析:
|
证法一:由已知条件知,⊿ABC和⊿AMN 都是等腰三角形(A为共公顶点)过点A作BC所在直线的垂线M,根据“三线合一”定理可知,这两个等腰三角形底边上的中线和顶角的平分线均在M上,而且这条直线是它们共公的对称轴所以B、C关于M对称,M、N关于M对称,所以BM=CN(轴对称性质) 证法二:∵AB=AC,AM=AN ∴∠ABC=∠ACB,∠M=∠N(等边对等角) ∴∠ABM=∠ACN(等角的补角相等) ∴∠BAM=∠CAN(三角形内角和定理) 在⊿ABM和⊿ACN中 ∴⊿ABM≌⊿ACN(ASA) ∴BM=CN(全等三角形对应边相等) |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

