题目内容
如图，已知直线l1，l2和△ABC，且l1⊥l2于点O．点A在l1上，点B、点C在l2上．（1）作△A1B1C1，使△A1B1C1与△ABC关于直线l1对称．
（2）作△A2B2C2，使△A2B2C2与△A1B1C1关于直线l2对称．
（3）△ABC与△A2B2C2有什么样的关系？
分析：（1）在直线l2上截取OB1=OB，OC1=OC，A1与A重合，然后顺次连接A1、B1、C1即可；
（2）在直线l1上截取OA2=OA，B2、C2分别B1、C1与重合，然后顺次连接A2、B2、C2即可；
（3）观察图形可知两三角形关于点O对称．
（2）在直线l1上截取OA2=OA，B2、C2分别B1、C1与重合，然后顺次连接A2、B2、C2即可；
（3）观察图形可知两三角形关于点O对称．
解答：解：（1）△A1B1C1如图所示；
（2）△A2B2C2如图所示；
（3））△ABC与△A2B2C2关于点O成中心对称．
（2）△A2B2C2如图所示；
（3））△ABC与△A2B2C2关于点O成中心对称．
点评：本题考查了利用轴对称变换作图，准确找出对应点的位置是解题的关键．
练习册系列答案
相关题目
6、如图，已知直线l1，l2，l3相交于点O，∠1=35°，∠2=25°，则∠3等于（ ）
（2012•郯城县一模）如图，已知直线l1∥l2∥l3∥l4，相邻两条平行直线间的距离都是1，如果正方形ABCD的四个顶点分别在四条直线上，则cosα=（ ）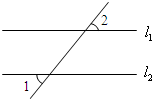
（2007•黔南州）如图，已知直线l1∥l2，∠1=50°，那么∠2=
如图：已知直线l1∥l2，且l3、l4和l1、l2分别交于点A、B和点C、D，点P在AB上，设∠ADP=∠1，∠DPC=∠2，∠BCP=∠3．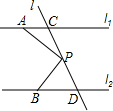
如图，已知直线l1∥l2，直线l3和直线l1、l2交于点C和D，在直线l3上有点P（点P与点C、D不重合），点A在直线l1上，点B在直线l2上．