题目内容
如图,四边形ABCD为平行四边形纸片.把纸片ABCD折叠,使点B恰好落在CD边上,折痕为AF.且AB=10cm、AD=8cm、DE=6cm.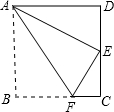 (1)求证:平行四边形ABCD是矩形;
(1)求证:平行四边形ABCD是矩形;(2)求BF的长;
(3)求折痕AF长.
分析:(1)根据翻折变换的对称性可知AE=AB,在△ADE中,利用勾股定理逆定理证明三角形为直角三角形,再根据有一个角是直角的平行四边形是矩形证明即可;
(2)设BF为x,分别表示出EF、EC、FC,然后在△EFC中利用勾股定理列式进行计算即可;
(3)在Rt△ABF中,利用勾股定理求解即可.
(2)设BF为x,分别表示出EF、EC、FC,然后在△EFC中利用勾股定理列式进行计算即可;
(3)在Rt△ABF中,利用勾股定理求解即可.
解答:(1)证明:∵把纸片ABCD折叠,使点B恰好落在CD边上,
∴AE=AB=10,AE2=102=100,
又∵AD2+DE2=82+62=100,
∴AD2+DE2=AE2,
∴△ADE是直角三角形,且∠D=90°,
又∵四边形ABCD为平行四边形,
∴平行四边形ABCD是矩形(有一个角是直角的平行四边形是矩形);
(2)解:设BF=x,则EF=BF=x,EC=CD-DE=10-6=4cm,FC=BC-BF=8-x,
在Rt△EFC中,EC2+FC2=EF2,
即42+(8-x)2=x2,
解得x=5,
故BF=5cm;
(3)解:在Rt△ABF中,由勾股定理得,AB2+BF2=AF2,
∵AB=10cm,BF=5cm,
∴AF=
=5
cm.
∴AE=AB=10,AE2=102=100,
又∵AD2+DE2=82+62=100,
∴AD2+DE2=AE2,
∴△ADE是直角三角形,且∠D=90°,
又∵四边形ABCD为平行四边形,
∴平行四边形ABCD是矩形(有一个角是直角的平行四边形是矩形);
(2)解:设BF=x,则EF=BF=x,EC=CD-DE=10-6=4cm,FC=BC-BF=8-x,
在Rt△EFC中,EC2+FC2=EF2,
即42+(8-x)2=x2,
解得x=5,
故BF=5cm;
(3)解:在Rt△ABF中,由勾股定理得,AB2+BF2=AF2,
∵AB=10cm,BF=5cm,
∴AF=
| 102+52 |
| 5 |
点评:本题主要考查了平行四边形的性质,矩形的判定,勾股定理,以及翻折变换前后的两个图形全等的性质,是综合题,但难度不大.

练习册系列答案
相关题目
 如图,四边形ABCD的对角线AC与BD互相垂直平分于点O,设AC=2a,BD=2b,请推导这个四边形的性质.(至少3条)
如图,四边形ABCD的对角线AC与BD互相垂直平分于点O,设AC=2a,BD=2b,请推导这个四边形的性质.(至少3条) 如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+CF.
如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+CF. 如图,四边形ABCD,AB=AD=2,BC=3,CD=1,∠A=90°,求∠ADC的度数.
如图,四边形ABCD,AB=AD=2,BC=3,CD=1,∠A=90°,求∠ADC的度数. 如图,四边形ABCD为正方形,E是BC的延长线上的一点,且AC=CE,求∠DAE的度数.
如图,四边形ABCD为正方形,E是BC的延长线上的一点,且AC=CE,求∠DAE的度数.