题目内容
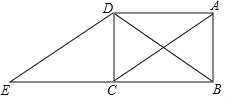
【题目】如图,在矩形ABCD中,连接对角线AC、BD,将△ABC沿BC方向平移,使点B移到点C,得到△DCE.
(1)求证:△ACD≌△EDC;
(2)请探究△BDE的形状,并说明理由.
【答案】(1)证明见解析(2)△BDE是等腰三角形
【解析】
试题分析:(1)由矩形的性质得出AB=DC,AC=BD,AD=BC,∠ADC=∠ABC=90°,由平移的性质得:DE=AC,CE=BC,∠DCE=∠ABC=90°,DC=AB,得出AD=EC,由SAS即可得出结论;
(2)由AC=BD,DE=AC,得出BD=DE即可.
试题解析:(1)∵四边形ABCD是矩形,
∴AB=DC,AC=BD,AD=BC,∠ADC=∠ABC=90°,
由平移的性质得:DE=AC,CE=BC,∠DCE=∠ABC=90°,DC=AB,
∴AD=EC,
在△ACD和△EDC中, ,
,
∴△ACD≌△EDC(SAS);
(2)△BDE是等腰三角形;理由如下:
∵AC=BD,DE=AC,
∴BD=DE,
∴△BDE是等腰三角形.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
