题目内容
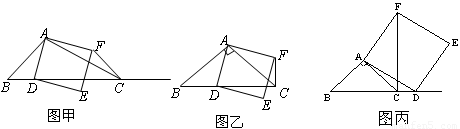
如图甲,在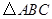 中,
中,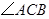 为锐角,点
为锐角,点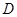 为射线
为射线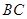 上一点,连接
上一点,连接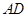 ,以
,以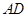 为一边且在
为一边且在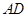 的右侧作正方形
的右侧作正方形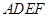 .解答下列问题:
.解答下列问题:
(1)如果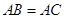 ,
,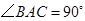 ,
,
①当点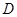 在线段
在线段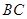 上时(与点
上时(与点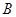 不重合),如图乙,线段
不重合),如图乙,线段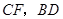 之间的位置关系为 ,数量关系为 .
之间的位置关系为 ,数量关系为 .
②当点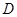 在线段
在线段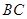 的延长线时,如图丙,①中的结论是否仍然成立,为什么?
的延长线时,如图丙,①中的结论是否仍然成立,为什么?
(2)如果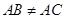 ,
,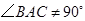 ,点
,点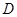 在线段
在线段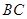 上运动.试探究:当
上运动.试探究:当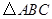 满足一个什么条件时,
满足一个什么条件时,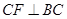 (点
(点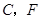 重合除外)?画出图形,并说明理由.(画图不写作法).
重合除外)?画出图形,并说明理由.(画图不写作法).
(1)①位置关系:互相垂直;数量关系:BD=CF;②成立;(2)∠ACB=45°
【解析】
试题分析:(1)当点D在BC的延长线上时①的结论仍成立.由正方形ADEF的性质可推出△DAB≌△FAC,所以CF=BD,∠ACF=∠ABD.结合∠BAC=90°,AB=AC,得到∠BCF=∠ACB+∠ACF=90度.即CF⊥BD.
(2)当∠ACB=45°时,过点A作AG⊥AC交CB或CB的延长线于点G,则∠GAC=90°,可推出∠ACB=∠AGC,所以AC=AG,由(1)①可知CF⊥BD.
(1)线段 之间的位置关系:互相垂直;数量关系:BD=CF;
之间的位置关系:互相垂直;数量关系:BD=CF;
②∵∠FAD=∠BAC=90°
∴∠BAD=∠CAF
在△BAD与△CAF中,
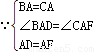
∴△BAD≌△CAF(SAS)
∴CF=BD,∠ACF=∠ACB=45°,
∴∠BCF=90°
∴CF⊥BD ;
(2)当∠ACB=45°时可得CF⊥BC,理由如下:
过点A作AC的垂线与CB所在直线交于G
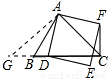
则∵∠ACB=45°
∴AG=AC∠AGC=∠ACG=45°
∵AG=AC,AD=AF,
∵∠GAD=∠GAC-∠DAC=90°-∠DAC,∠FAC=∠FAD-∠DAC=90°-∠DAC,
∴∠GAD=∠FAC,
∴△GAD≌△CAF(SAS)
∴∠ACF=∠AGD=45°
∴∠GCF=∠GCA+∠ACF=90°
∴CF⊥BC.
考点:三角形全等的判定和直角三角形的判定
点评:判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.




 中,
中,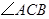 为锐角,点
为锐角,点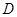 为射线
为射线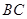 上一点,连接
上一点,连接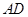 ,以
,以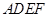 .解答下列问题:
.解答下列问题: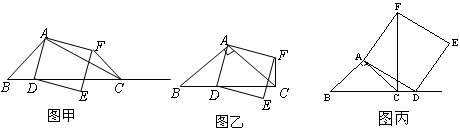
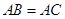 ,
,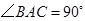 ,
, 不重合),如图乙,线段
不重合),如图乙,线段 之间的位置关系为 ,数量关系为 .
之间的位置关系为 ,数量关系为 .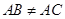 ,
,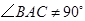 ,点
,点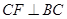 (点
(点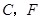 重合除外)?画出图形,并说明理由.(画图不写作法).
重合除外)?画出图形,并说明理由.(画图不写作法).