题目内容
【题目】从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中有一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线。
(1)如图1,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD为△ABC的完美分割线;
(2)在△ABC中,∠A=48°,CD是△ABC的完美分割线,且△ACD为等腰三角形,求∠ACB的度数;
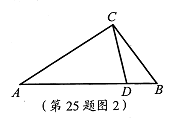
(3)如图2,△ABC中,AC=2,BC=![]() ,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长。
,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长。

【答案】(1)详见解析;(2)∠ACB=96°或114°;(3)CD=![]() .
.
【解析】
试题分析:(1)由∠A=40°,∠B=60°可得∠ACB=80°,即△ABC不是等腰三角形,再判定△ACD是等腰三角形,△BCD∽△BAC,即可得CD为△ABC的完美分割线;(2)分AD=CD,AD=AC,AC=CD三种情况,根据这三种情况分别求出∠ACB的度数,不合题意的舍去;(3)由△BCD∽△BAC可得![]() ,设BD=x,代入可得
,设BD=x,代入可得![]() ,由于x>0,即可知x=
,由于x>0,即可知x=![]() -1.再由△BCD∽△BAC,所以
-1.再由△BCD∽△BAC,所以![]() ,解得CD=
,解得CD=![]() .
.
试题解析:(1)∵∠A=40°,∠B=60°,
∴∠ACB=80°,
∴△ABC不是等腰三角形,
又因CD为角平分线,
∴∠ACD=∠BCD=![]() ∠ABC=40°,
∠ABC=40°,
∴∠ACD=∠A=40°,
∴△ACD是等腰三角形,
∵∠BCD=∠A=40°,∠B=∠B,
∴△BCD∽△BAC,
∴CD为△ABC的完美分割线;
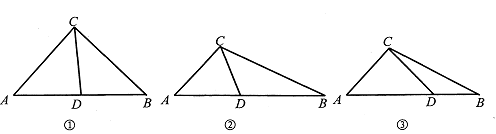
(2)当AD=CD时(如图①),∠ACD=∠A=48°,
∵△BDC∽△BCA,
∴∠BCD=∠A=48°,
∴∠ACB=∠ACD+∠BCD=96°;
当AD=AC时(如图②),∠ACD=∠ADC=![]() ,
,
∵△BDC∽△BCA,
∴∠BCD=∠A=48°,
∴∠ACB=∠ACD+∠BCD=114°;
当AC=CD时(如图③),∠ACD=∠A=48°,
∵△BDC∽△BCA,
∴∠BCD=∠A=48°,
∵∠ADC>∠BCD,矛盾,舍去.
∴∠ACB=96°或114°;
(3)由已知AC=AD=2,
∵△BCD∽△BAC,
∴![]() ,
,
设BD=x
∴![]()
解得x=-1±![]() ,
,
∵x>0,
∴x=![]() -1.
-1.
∵△BCD∽△BAC,
∴![]() ,
,
∴CD=![]() .
.

 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案