题目内容
在△ABC中,AD⊥BC于D,AD=4,BD:DC=1:2,将Rt△ABD绕点A逆时针旋转90°,得△AEF,E、F分别是B、D的对应点,FE(或延长线)交BC(或延长线)于H,过点C作CG∥AD交AF(或延长线)于G,设BD=x(x>0).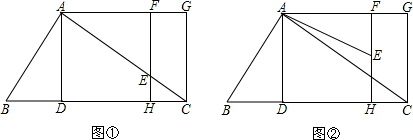
(1)如图①,当点E恰好落在边AC上时,求BD的长;
(2)如图②,若点F在AG上,试讨论以F为圆心,FE长为半径的⊙F与CG所在直线的位置关系;
(3)求当0<x<2
| 2 |
分析:(1)根据旋转的性质,可得△AEF≌△ABD,易证△AEF∽△ACG,根据比例的性质,表示各量,可解答;
(2)由F在AG上,可得2x≥4,FG=2x-4,当FG=EF,FG>EF,FG<EF分类讨论其位置关系;
(3)根据当0<x≤2和2<x<2
时,EF与CG的位置关系,结合四边形ADCE的形状,分类求其解析式,解答出即可;
(2)由F在AG上,可得2x≥4,FG=2x-4,当FG=EF,FG>EF,FG<EF分类讨论其位置关系;
(3)根据当0<x≤2和2<x<2
| 2 |
解答: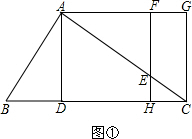 (1)证明:如图①,
(1)证明:如图①,
∵△AEF是由△ABD绕点A逆时针旋转90°所得,
∴△AEF≌△ABD,
∴∠ADB=∠AFE=90°,
∴AD∥CG∥EF,
由已知,E在AC上,
∴△AEF∽△ACG,
∴
=
,
由AF=4,AG=2x,EF=x,CG=4,
∴
=
解得x=2
,
∴BD=2
;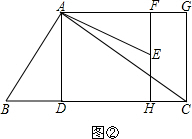
(2)解:如图②,
∵F在AG上,
∴2x≥4即x≥2,FG=2x-4,由已知CG⊥AF,
∴当FG=EF时,即2x-4=x,x=4,
∴当x=4时,⊙F与CG所在直线相切,
当2≤x<4时,⊙F与CG所在直线相交,
当x>4时,⊙F与CG所在直线相离;
(3)
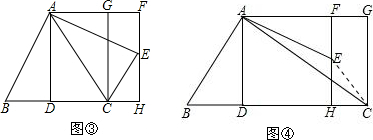
①如图③,
当0<x≤2时,AG=DC=2x<AF=4,
∴G在AF上
∴S四边形ADCE=S矩形ADHF-S△AEF-S△CHE,
=16-
×4x-
(4-x)(4-2x),
=16-2x-8+6x-x2,
=-x2+4x+8;
②当2<x<2
时,AG=DC=2x>AF,
∴G在AF延长线上,
S四边形ADCE=S梯形ADHE+S△HCE,
=
(4+4-x)×4+
(2x-4)(4-x),
=16-2x-x2+6x-8,
=-x2+4x+8;
综上,S四边形ADCE=-x2+4x+8(0<x<2
).
 (1)证明:如图①,
(1)证明:如图①,∵△AEF是由△ABD绕点A逆时针旋转90°所得,
∴△AEF≌△ABD,
∴∠ADB=∠AFE=90°,
∴AD∥CG∥EF,
由已知,E在AC上,
∴△AEF∽△ACG,
∴
| CG |
| EF |
| AG |
| AF |
由AF=4,AG=2x,EF=x,CG=4,
∴
| 4 |
| x |
| 2x |
| 4 |
| 2 |
∴BD=2
| 2 |

(2)解:如图②,
∵F在AG上,
∴2x≥4即x≥2,FG=2x-4,由已知CG⊥AF,
∴当FG=EF时,即2x-4=x,x=4,
∴当x=4时,⊙F与CG所在直线相切,
当2≤x<4时,⊙F与CG所在直线相交,
当x>4时,⊙F与CG所在直线相离;
(3)

①如图③,
当0<x≤2时,AG=DC=2x<AF=4,
∴G在AF上
∴S四边形ADCE=S矩形ADHF-S△AEF-S△CHE,
=16-
| 1 |
| 2 |
| 1 |
| 2 |
=16-2x-8+6x-x2,
=-x2+4x+8;
②当2<x<2
| 2 |
∴G在AF延长线上,
S四边形ADCE=S梯形ADHE+S△HCE,
=
| 1 |
| 2 |
| 1 |
| 2 |
=16-2x-x2+6x-8,
=-x2+4x+8;
综上,S四边形ADCE=-x2+4x+8(0<x<2
| 2 |
点评:本题考查了旋转的性质、相似三角形的判定和性质、直线与圆的位置关系及二次函数关系式的求法;考查的知识点较多,考查了学生对知识掌握程度及熟练应用所学知识的能力.

练习册系列答案
相关题目
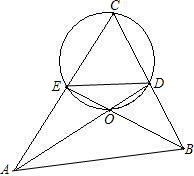 如图,在△ABC中,AD,BE分别是∠A,∠B的角平分线,O是AD与BE的交点,若C,D,O,E四点共圆,DE=3,则△ODE的内切圆半径为
如图,在△ABC中,AD,BE分别是∠A,∠B的角平分线,O是AD与BE的交点,若C,D,O,E四点共圆,DE=3,则△ODE的内切圆半径为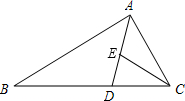 如图,在△ABC中,AD是角平分线,E是AD上的一点,且CE=CD.
如图,在△ABC中,AD是角平分线,E是AD上的一点,且CE=CD.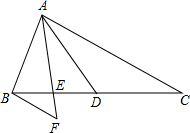 (2012•松江区一模)已知:如图,在△ABC中,AD是边BC上的中线,点E在线段BD上,且BE=ED,过点B作BF∥AC,交线段AE的延长线于点F.
(2012•松江区一模)已知:如图,在△ABC中,AD是边BC上的中线,点E在线段BD上,且BE=ED,过点B作BF∥AC,交线段AE的延长线于点F.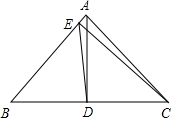 (2013•海珠区一模)如图,在△ABC中,AD、CE分别是BC、AB边上的高,DE=3,BE=4,BC=6,则AC=
(2013•海珠区一模)如图,在△ABC中,AD、CE分别是BC、AB边上的高,DE=3,BE=4,BC=6,则AC= 如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,已知EH=EB=3,AE=4,则CH的长是
如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,已知EH=EB=3,AE=4,则CH的长是