题目内容
下列命题中:①正多边形都是轴对称图形;②同位角一定相等;③一边上的中线等于这条边的一半的三角形一定是直角三角形;④对角线相等的平行四边形是菱形;⑤若关于x的方程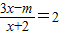 的解是负数,则m的取值范围为m<-4,其中正确的个数是( )
的解是负数,则m的取值范围为m<-4,其中正确的个数是( )A.2个
B.3个
C.4个
D.5个
【答案】分析:根据正多边形的性质对①进行判断;根据平行线的性质对②进行判断;利用圆周角定理的推论可对③进行判断;根据菱形的判定方法对④进行判断;解分式方程得到m<-4且m≠-6,于是可对⑤进行判断.
解答:解:正多边形都是轴对称图形,对称轴的条数等于边数,所以①正确;
两直线平行,同位角相等,所以②错误;
一边上的中线等于这条边的一半的三角形一定是直角三角形,所以③正确;
对角线相互垂直的平行四边形是菱形,所以④错误;
去分母得3x-m=2x+4,解得x=m+4,因为原方程的解为负数,所以m+4<0且m+4≠-2,所以m的取值范围为m<-4且m≠-6,所以⑤错误.
故选A.
点评:本题考查了命题:判断事物的语句叫命题;正确的命题叫真命题,错误的命题叫假命题;经过推理论证的真命题叫定理.
解答:解:正多边形都是轴对称图形,对称轴的条数等于边数,所以①正确;
两直线平行,同位角相等,所以②错误;
一边上的中线等于这条边的一半的三角形一定是直角三角形,所以③正确;
对角线相互垂直的平行四边形是菱形,所以④错误;
去分母得3x-m=2x+4,解得x=m+4,因为原方程的解为负数,所以m+4<0且m+4≠-2,所以m的取值范围为m<-4且m≠-6,所以⑤错误.
故选A.
点评:本题考查了命题:判断事物的语句叫命题;正确的命题叫真命题,错误的命题叫假命题;经过推理论证的真命题叫定理.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 的解是负数,则m的取值范围为m<-4,其中正确的个数是
的解是负数,则m的取值范围为m<-4,其中正确的个数是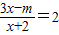 的解是负数,则m的取值范围为m<-4,其中正确的个数是( )
的解是负数,则m的取值范围为m<-4,其中正确的个数是( )