Question

如图，在梯形ABCD中，AD∥BC，AD=2，BC=4，点M是AD的中点，△MBC是等边三角形．动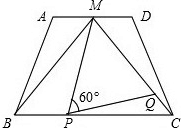点P、Q分别是在线段BC和MC上运动，且∠MPQ=60°保持不变．
（1）求证：梯形ABCD是等腰梯形；
（2）设PC为x，MQ=y，求y与x的函数关系式，并写出自变量取值范围；
（3）在（2）中，当y取最小值时，判断△PQC的形状，并说明理由．

Answer 1

分析：（1）需证△AMB≌△DMC，可得AB=DC，可得梯形ABCD是等腰梯形；
（2）可证△BPM∽△CQP，则PC：BM=CQ：BP，PC=x，MQ=y，BP=4-x，QC=4-y，即可得到BP与CQ的关系，从而转化成y与x的函数关系式；
（3）先利用二次函数求最值，求出y取最小值时x的值和y的最小值，从而确定P、Q的位置，判断出△PQC的形状．

解答：解：（1）证明：∵△MBC是等边三角形，
∴MB=MC，∠MBC=∠MCB=60°，
∵M是AD中点，
∴AM=MD
∵AD∥BC，
∴∠AMB=∠MBC=60°，∠DMC=∠MCB=60°．
∴△AMB≌△DMC，（2分）
∴AB=DC，
∴梯形ABCD是等腰梯形．（3分）

（2）在等边三角形MBC中，MB=MC=BC=4，∠MBC=∠MCB=60°，∠MPQ=60°，
∴∠BMP+∠BPM=∠BPM+∠QPC=120°，
∴∠BMP=∠QPC，
∴△BMP∽△CPQ，
∴PC：BM=CQ：BP（5分）
∵PC=x，MQ=y，则BP=4-x，QC=4-y，
∴

x

4

=

4-y

4-x

，
∴y=

1

4

x²-x+4（0＜x＜4）
（3）△PQC为直角三角形，
由（2）知，当MQ取最小值时，x=PC=2．
∴P是BC的中点，MP⊥BC，而∠MPQ=60°，
∴∠CPQ=30°，
∴∠PQC=90°，
∴△PQC是直角三角形．

点评：本题考查了本题考查平行四边形、直角三角形和等腰梯形的判定以及相似三角形的判定和性质的应用．还考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养，求函数最小值等知识点．要会利用数形结合的思想把代数和几何图形结合起来．