题目内容
如图,抛物线y= x2-mx+n与x轴交于A、B两点,与y轴交于点C(0.-1).且对称轴x=l.
x2-mx+n与x轴交于A、B两点,与y轴交于点C(0.-1).且对称轴x=l.(1)求出抛物线的解析式及A、B两点的坐标;
(2)在x轴下方的抛物线上是否存在点D,使四边形ABDC的面积为3?若存在,求出点D的坐标;若不存在.说明理由(使用图1);
(3)点Q在y轴上,点P在抛物线上,要使Q、P、A、B为顶点的四边形是平行四边形,请求出所有满足条件的点P的坐标(使用图2).

【答案】分析:(1)根据二次函数对称轴公式以及二次函数经过(0.-1)点即可得出答案;
(2)根据S四边形ABDC=S△AOC+S梯形OCDM+S△BMD,表示出关于a的一元二次方程求出即可;
(3)分别从当AB为边时,只要PQ∥AB,且PQ=AB=4即可以及当AB为对角线时,只要线段PQ与线段AB互相平分即可,分别求出即可.
解答:解:(1)∵抛物线与y轴交于点C(0.-1).且对称轴x=l.
∴ ,解得:
,解得: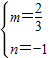 ,
,
∴抛物线解析式为y= x2-
x2- x-1,
x-1,
令 x2-
x2- x-1=0,得:x1=-1,x2=3,
x-1=0,得:x1=-1,x2=3,
∴A(-1,0),B(3,0),
(2)设在x轴下方的抛物线上存在D(a,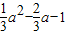 )(0<a<3)使四边形ABCD的面积为
)(0<a<3)使四边形ABCD的面积为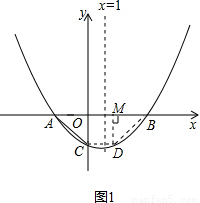 3.
3.
作DM⊥x轴于M,则S四边形ABDC=S△AOC+S梯形OCDM+S△BMD,
∴S四边形ABDC= |xAyC|+
|xAyC|+ (|yD|+|yC|)xM+
(|yD|+|yC|)xM+ (xB-xM)|yD|
(xB-xM)|yD|
= ×1×1+
×1×1+ [-(
[-( a2-
a2- a-1)+1]×a+
a-1)+1]×a+ (3-a)[-(
(3-a)[-( a2-
a2- a-1)]
a-1)]
=- a2+
a2+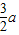 +2,
+2,
∴由- a2+
a2+ +2=3,
+2=3,
解得:a1=1,a2=2,
∴D的纵坐标为: a2-
a2- a-1=-
a-1=- 或-1,
或-1,
∴点D的坐标为(1,- ),(2,-1);
),(2,-1);
(3)①当AB为边时,只要PQ∥AB,且PQ=AB=4即可,又知点Q在y轴上,所以点P的横坐标为-4或4,
当x=-4时,y=7;当x=4时,y= ;
;
所以此时点P1的坐标为(-4,7),P2的坐标为(4, );
);
②当AB为对角线时,只要线段PQ与线段AB互相平分即可,线段AB中点为G,PQ必过G点且与y轴交于Q点,
过点P3作x轴的垂线交于点H,
可证得△P3HG≌△Q3OG,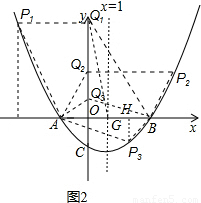
∴GO=GH,
∵线段AB的中点G的横坐标为1,
∴此时点P横坐标为2,
由此当x=2时,y=-1,
∴这是有符合条件的点P3(2,-1),
∴所以符合条件的点为:P1的坐标为(-4,7),P2的坐标为(4, );P3(2,-1).
);P3(2,-1).
点评:此题主要考查了二次函数的综合应用,二次函数的综合应用是初中阶段的重点题型,特别注意利用数形结合是这部分考查的重点,也是难点,同学们应重点掌握.
(2)根据S四边形ABDC=S△AOC+S梯形OCDM+S△BMD,表示出关于a的一元二次方程求出即可;
(3)分别从当AB为边时,只要PQ∥AB,且PQ=AB=4即可以及当AB为对角线时,只要线段PQ与线段AB互相平分即可,分别求出即可.
解答:解:(1)∵抛物线与y轴交于点C(0.-1).且对称轴x=l.
∴
 ,解得:
,解得: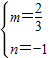 ,
,∴抛物线解析式为y=
 x2-
x2- x-1,
x-1,令
 x2-
x2- x-1=0,得:x1=-1,x2=3,
x-1=0,得:x1=-1,x2=3,∴A(-1,0),B(3,0),
(2)设在x轴下方的抛物线上存在D(a,
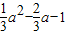 )(0<a<3)使四边形ABCD的面积为
)(0<a<3)使四边形ABCD的面积为 3.
3.作DM⊥x轴于M,则S四边形ABDC=S△AOC+S梯形OCDM+S△BMD,
∴S四边形ABDC=
 |xAyC|+
|xAyC|+ (|yD|+|yC|)xM+
(|yD|+|yC|)xM+ (xB-xM)|yD|
(xB-xM)|yD|=
 ×1×1+
×1×1+ [-(
[-( a2-
a2- a-1)+1]×a+
a-1)+1]×a+ (3-a)[-(
(3-a)[-( a2-
a2- a-1)]
a-1)]=-
 a2+
a2+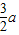 +2,
+2,∴由-
 a2+
a2+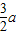 +2=3,
+2=3,解得:a1=1,a2=2,
∴D的纵坐标为:
 a2-
a2- a-1=-
a-1=- 或-1,
或-1,∴点D的坐标为(1,-
 ),(2,-1);
),(2,-1);(3)①当AB为边时,只要PQ∥AB,且PQ=AB=4即可,又知点Q在y轴上,所以点P的横坐标为-4或4,
当x=-4时,y=7;当x=4时,y=
 ;
;所以此时点P1的坐标为(-4,7),P2的坐标为(4,
 );
);②当AB为对角线时,只要线段PQ与线段AB互相平分即可,线段AB中点为G,PQ必过G点且与y轴交于Q点,
过点P3作x轴的垂线交于点H,
可证得△P3HG≌△Q3OG,

∴GO=GH,
∵线段AB的中点G的横坐标为1,
∴此时点P横坐标为2,
由此当x=2时,y=-1,
∴这是有符合条件的点P3(2,-1),
∴所以符合条件的点为:P1的坐标为(-4,7),P2的坐标为(4,
 );P3(2,-1).
);P3(2,-1).点评:此题主要考查了二次函数的综合应用,二次函数的综合应用是初中阶段的重点题型,特别注意利用数形结合是这部分考查的重点,也是难点,同学们应重点掌握.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
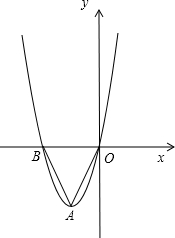 如图,抛物线y=x2+4x与x轴分别相交于点B、O,它的顶点为A,连接AB,AO.
如图,抛物线y=x2+4x与x轴分别相交于点B、O,它的顶点为A,连接AB,AO. 16、如图,抛物线y=-x2+2x+m(m<0)与x轴相交于点A(x1,0)、B(x2,0),点A在点B的左侧.当x=x2-2时,y
16、如图,抛物线y=-x2+2x+m(m<0)与x轴相交于点A(x1,0)、B(x2,0),点A在点B的左侧.当x=x2-2时,y 已知如图,抛物线y=x2+(k2+1)x+k+1的对称轴是直线x=-1,且顶点在x轴上方.设M是直线x=-1左侧抛物线上的一动点,过点M作x轴的垂线MG,垂足为G,过点M作直线x=-1的垂线MN,垂足为N,直线x=-1与x轴的交于H点,若M点的横坐标为x,矩形MNHG的周长为l.
已知如图,抛物线y=x2+(k2+1)x+k+1的对称轴是直线x=-1,且顶点在x轴上方.设M是直线x=-1左侧抛物线上的一动点,过点M作x轴的垂线MG,垂足为G,过点M作直线x=-1的垂线MN,垂足为N,直线x=-1与x轴的交于H点,若M点的横坐标为x,矩形MNHG的周长为l. (2013•扬州)如图,抛物线y=x2-2x-8交y轴于点A,交x轴正半轴于点B.
(2013•扬州)如图,抛物线y=x2-2x-8交y轴于点A,交x轴正半轴于点B.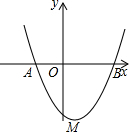 如图,抛物线y=x2-2x-3与x轴分别交于A,B两点.
如图,抛物线y=x2-2x-3与x轴分别交于A,B两点.