题目内容
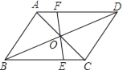
【题目】在矩形ABCD中,点E、F分别在AB、AD上,∠EFB=2∠AFE=2∠BCE,CD=9,CE=20,则线段AF的长为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
如图,取CE的中点H,连接BH,设∠EFB=2∠AFE=2∠ECB=2a,则∠AFB=3a,进而求出BH=CH=EH=10,∠HBC=∠HCB=a,再根据AD∥BC求出EF∥BH,进而得出△EFG和△BGH均为等腰三角形,则BF=EH=10,再根据勾股定理即可求解.
如图,取CE的中点H,连接BH,设∠EFB=2∠AFE=2∠ECB=2a,则∠AFB=3a,

∵在矩形ABCD中有AD∥BC,∠A=∠ABC=90°,
∴△BCE为直角三角形,
∵点H为斜边CE的中点,CE=20,
∴BH=CH=EH=10,∠HBC=∠HCB=a,
∵AD∥BC,
∴∠AFB=∠FBC=3a,
∴∠GBH=3a-a=2a=∠EFB,
∴EF∥BH,
∴∠FEG=∠GHB=∠HBC+∠HCB=2a=∠EFB=∠GBH,
∴△EFG和△BGH均为等腰三角形,
∴BF=EH=10,
∵AB=CD=9,
∴![]() .
.
故选C.

练习册系列答案
相关题目